题目内容
9.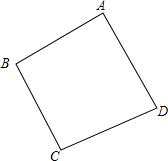 如图所示,某市为加快“工业立市”的步伐,计划在四边形工业区ABCD中建立一个土特产中转站O,使点O到A,B,C,D四点的连线之和最小,请你找出点O.
如图所示,某市为加快“工业立市”的步伐,计划在四边形工业区ABCD中建立一个土特产中转站O,使点O到A,B,C,D四点的连线之和最小,请你找出点O.
分析 连接AC、BD相交于点O,则点O就是所要找的点;取不同于点P的任意一点P,连接PA、PB、PC、PD,根据三角形任意两边之和大于第三边可得PA+PC>AC,PB+PD>BD,然后结合图形即可得到PA+PB+PC+PD>OA+OB+OC+OD,从而可得点O就是所要找的四边形ABCD内符合要求的点.
解答 解:如图,要使OA+OB+OC+OD最小,则点O是线段AC、BD的交点.
理由如下:如果存在不同于点O的交点P,连接PA、PB、PC、PD,
那么PA+PC>AC,
即PA+PC>OA+OC,
同理,PB+PD>OB+OD,
则PA+PB+PC+PD>OA+OB+OC+OD,
即点O是线段AC、BD的交点时,OA+OB+OC+OD之和最小.
点评 本题考查了三角形的任意两边之和大于第三边的性质,作出图形更助于问题的解决,本题渗透了反证法的思想,希望同学们逐渐适应并熟练掌握.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
17.甲乙两人做划拳走步游戏,从同一起点出发,每对决一次,赢的人向正方向走,输的人向负方向走,规定:向东前进为正,向西后退为负,游戏记录如下(单位:米)
(1)游戏结束后,甲在乙什么方位?相距多远?
(2)甲乙共走了多少米?
(3)在游戏中,若前进2米奖励一颗糖,则甲可得到几颗糖?
| 甲 | -2 | +1 | -2 | +2 | +3 | +1 | +1 |
| 乙 | +1 | -2 | +1 | -4 | -6 | -2 | -2 |
(2)甲乙共走了多少米?
(3)在游戏中,若前进2米奖励一颗糖,则甲可得到几颗糖?
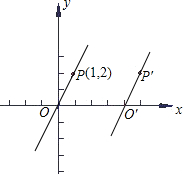 如图.正比例函数y=kx经过点P(1,2).
如图.正比例函数y=kx经过点P(1,2).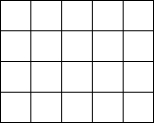 小猫在如图的地砖上随意走动,它停在任一块方砖上的机会均等,现在知道小猫停在红色方砖上的概率是$\frac{1}{4}$,试把红色方砖的颜色涂上阴影.
小猫在如图的地砖上随意走动,它停在任一块方砖上的机会均等,现在知道小猫停在红色方砖上的概率是$\frac{1}{4}$,试把红色方砖的颜色涂上阴影. (1)如图①,在半径为2的⊙O中,∠AOB=45°,
(1)如图①,在半径为2的⊙O中,∠AOB=45°,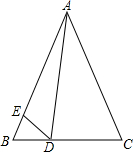 如图,在△ABC中,AB=AC,点D、E分别在BC、AB上,且∠BDE=∠CAD.△ADE与△ABD相似吗?为什么?
如图,在△ABC中,AB=AC,点D、E分别在BC、AB上,且∠BDE=∠CAD.△ADE与△ABD相似吗?为什么?