题目内容
11.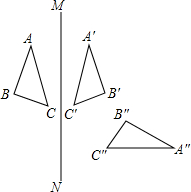 如图,△ABC和△A′B′C′关于直线MN对称,△A′B′C′和△A″B″C″关于直线EF对称.
如图,△ABC和△A′B′C′关于直线MN对称,△A′B′C′和△A″B″C″关于直线EF对称.(1)画出直线EF;
(2)直线MN与EF相交于点O,试探究∠BOB″与直线MN、EF所夹锐角α的数量关系;
(3)你能否将△ABC经过一次变换得到△A″B″C″?如果能,请说说你是如何变换的?如果不能,请说明理由.
分析 (1)作B′B″的垂直平分线即可得到EF;
(2)利用轴对称性质得到∠BOM=∠B′OM,∠B′OE=∠B″OE,则∠BOB″=2∠B′OM+2∠B′OE=2∠MOE;
(3)利用旋转变换求解.
解答 解:(1)如图,
(2)∠BOB″是直线MN、EF所夹锐角α的2倍.理由如下:
∵△ABC和△A′B′C′关于直线MN对称,
∴BO与B′O关于MN对称,
∴∠BOM=∠B′OM,
同理可得∠B′OE=∠B″OE,
∴∠BOB″=2∠B′OM+2∠B′OE=2∠MOE=2α;
(3)把△ABC绕点O顺时针旋转2α可得到△A″B″C″.
点评 本题考查了作图-轴对称变换:在画一个图形的轴对称图形时,也是先从确定一些特殊的对称点开始的,一般的方法是:先由已知点出发向所给直线作垂线,并确定垂足;再直线的另一侧,以垂足为一端点,作一条线段使之等于已知点和垂足之间的线段的长,得到线段的另一端点,即为对称点;然后连接这些对称点,就得到原图形的轴对称图形.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.小丰妈妈买了一部29英寸(74cm)电视机,下列对29英寸的说法中正确的是( )
| A. | 指的是屏幕的长度 | B. | 指的是屏幕的宽度 | ||
| C. | 指的是屏幕的周长 | D. | 是屏幕对角线的长度 |
3.有序数对(2x-1,5-3y)表示的点是(5,2),则x,y的值分别是( )
| A. | 2,5 | B. | -1,5 | C. | 3,1 | D. | 2,1 |
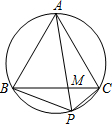 如图,点P为等边△ABC外接圆,劣弧为BC上的一点.
如图,点P为等边△ABC外接圆,劣弧为BC上的一点.