题目内容
5.从不等式2x-1<5,4x-1>3x-1,x-1≥2x中选取两个你喜欢的不等式,组成一个一元一次不等式组,解你所做到的这个不等式组,并把解集在数轴上表示出来.分析 先确定好不等式组.然后求出不等式组中各个不等式的解集,再利用数轴确定不等式组的解集.
解答 解:本题答案不唯一.
按要求选出两个不等式组成一个不等式组;
求出不等式组的解集;
在数轴上表示所求的解集.
由2x-1<5得x<3,
由4x-1>3x-1得x>0,
由x-1≥2x得x≤-1.
如果选择2x-1<5,4x-1>3x-1,则组成$\left\{\begin{array}{l}{2x-1<5}\\{4x-1>3x-1}\end{array}\right.$
解集为0<x<3.
在数轴上表示为 .
.
如果选择2x-1<5,x-1≥2x,则组成$\left\{\begin{array}{l}{2x-1<5}\\{x-1≥2x}\end{array}\right.$
解集为x≤-1.
在数轴上表示为 .
.
如果选择3x>0,x-1≥2x,则组成$\left\{\begin{array}{l}{4x-1>3x-1}\\{x-1≥2x}\end{array}\right.$
此不等式组无解.
在数轴上表示为
点评 本题考查了解一元一次不等式组,在数轴上表示不等式的解集.解不等式组时要注意解集的确定原则:同大取大,同小取小,大小小大取中间,大大小小无解了.

练习册系列答案
相关题目
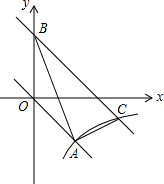 如图,在平面直角坐标系xOy中,正比例函数y=kx的图象与反比例函数y=$\frac{m}{x}$的图象都经过点A(2,-2).
如图,在平面直角坐标系xOy中,正比例函数y=kx的图象与反比例函数y=$\frac{m}{x}$的图象都经过点A(2,-2). 如图,CE是△ABC的外角∠ACD的平分线,交BA的延长线于点E,若∠E=20°,∠B=30°,则∠BAC=70°.
如图,CE是△ABC的外角∠ACD的平分线,交BA的延长线于点E,若∠E=20°,∠B=30°,则∠BAC=70°.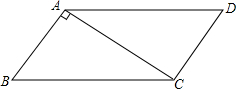 如图:在?ABCD中,CA⊥BA,AB=3,AC=4,求?ABCD的周长及面积.
如图:在?ABCD中,CA⊥BA,AB=3,AC=4,求?ABCD的周长及面积.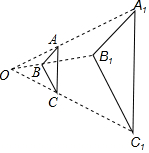 如图,△ABC与△A1B1C1是以点O为位似中心的位似图形,且位似比为1:3,若△A1B1C1面积为3,则△ABC的面积为$\frac{1}{3}$.
如图,△ABC与△A1B1C1是以点O为位似中心的位似图形,且位似比为1:3,若△A1B1C1面积为3,则△ABC的面积为$\frac{1}{3}$.