题目内容
1.将一张长方形的纸对折,如图所示可得到一条折痕(图中虚线),继续对折,对折时每次折痕与上次的折痕保持平行,连续对折8次后,可得到折痕条数为256.
分析 观察图形,对折1次,是2-1=1条折痕,对折2次22-1=3条折痕,对折3次23-1=7条折痕,对折4次24-1=15条折痕,…,据此可得,对折n次是2n-1条折痕,据此即可解答问题.
解答 解:∵对折1次,是2-1=1条折痕,
对折2次22-1=3条折痕,
对折3次23-1=7条折痕,
对折4次24-1=15条折痕,
…,
∴对折n次是2n-1条折痕,
当n=8时,折痕有:28-1=256(条)
答:如果对折八次后,可以得到256条折痕.
故答案为:256.
点评 此题考查了图形的变化规律,学生通过特例分析从而归纳总结出一般结论的能力.对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的,通过分析找到各部分的变化规律后直接利用规律求解.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
13.下列各式从左到右的变形中,属于因式分解的是( )
| A. | (a+b)(a-b)=a2-b2 | B. | a2+2ab+b2=(a+b)2 | C. | a(a+b)=a2+ab | D. | (a-b)2=(b-a)2 |
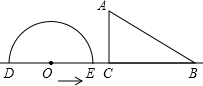 如图,形如量角器的半圆O的直径DE=12cm,形如三角形的△ABC中,∠ACB=90°,∠ABC=30°,BC=12cm,半圆O以2cm/s的速度从左向右运动,在运动过程中,点D、E始终在直线BC上,设运动时间为t(s),当t=0s时,半圆O在△ABC的左侧,OC=8cm.
如图,形如量角器的半圆O的直径DE=12cm,形如三角形的△ABC中,∠ACB=90°,∠ABC=30°,BC=12cm,半圆O以2cm/s的速度从左向右运动,在运动过程中,点D、E始终在直线BC上,设运动时间为t(s),当t=0s时,半圆O在△ABC的左侧,OC=8cm. 如图,圆A的半径为3,P是CB延长线上一点,PO=6,PA切圆O于点A,那么圆O的切线PA的长为3$\sqrt{3}$.
如图,圆A的半径为3,P是CB延长线上一点,PO=6,PA切圆O于点A,那么圆O的切线PA的长为3$\sqrt{3}$.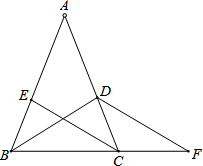 如图:∠ABC=∠ACB,BD平分∠ABC,CE平分∠ACB,∠DBF=∠F,那么EC与DF平行吗?为什么?请完成下面的解题过程.
如图:∠ABC=∠ACB,BD平分∠ABC,CE平分∠ACB,∠DBF=∠F,那么EC与DF平行吗?为什么?请完成下面的解题过程.