题目内容
16. 如图,圆A的半径为3,P是CB延长线上一点,PO=6,PA切圆O于点A,那么圆O的切线PA的长为3$\sqrt{3}$.
如图,圆A的半径为3,P是CB延长线上一点,PO=6,PA切圆O于点A,那么圆O的切线PA的长为3$\sqrt{3}$.
分析 先根据切线的性质得到OA⊥PA,然后利用勾股定理计算PA的长.
解答 解:∵PA切⊙O于A点,
∴OA⊥PA,
在Rt△OPA中,OP=6,OA=3,
∴PA=$\sqrt{{OP}^{2}{-OA}^{2}}$=3$\sqrt{3}$
故答案为:3$\sqrt{3}$.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径,勾股定理,熟记切线的性质是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11.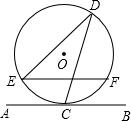 如图,如果直线AB与半径为2的⊙O相切于点C,D是⊙O上一点,且∠EDC=30°,弦EF∥AB,则EF的长是( )
如图,如果直线AB与半径为2的⊙O相切于点C,D是⊙O上一点,且∠EDC=30°,弦EF∥AB,则EF的长是( )
 如图,如果直线AB与半径为2的⊙O相切于点C,D是⊙O上一点,且∠EDC=30°,弦EF∥AB,则EF的长是( )
如图,如果直线AB与半径为2的⊙O相切于点C,D是⊙O上一点,且∠EDC=30°,弦EF∥AB,则EF的长是( )| A. | 2$\sqrt{3}$ | B. | 8 | C. | 2$\sqrt{10}$ | D. | 2$\sqrt{13}$ |
 如图,AB∥CD,EF分别交AB、CD与M、N,∠EMB=50°,MG平分∠BMF,MG交CD于G,求∠MGC的度数.
如图,AB∥CD,EF分别交AB、CD与M、N,∠EMB=50°,MG平分∠BMF,MG交CD于G,求∠MGC的度数.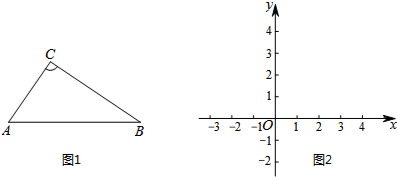
 如图是用棋子摆成的“T”字图案.从图案中可以看出,第1个“T”字型图案需要5枚棋子,第2个“T”字型图案需要8枚棋子,第3个“T”字型图案需要11枚棋子.
如图是用棋子摆成的“T”字图案.从图案中可以看出,第1个“T”字型图案需要5枚棋子,第2个“T”字型图案需要8枚棋子,第3个“T”字型图案需要11枚棋子.
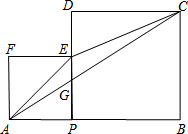 如图,AB=a,P是线段AB上任意一点(点P不与A、B重合),分别以AP,BP为边作正方形APEF、正方形PBCD,点E在边PD上.设AP=x.
如图,AB=a,P是线段AB上任意一点(点P不与A、B重合),分别以AP,BP为边作正方形APEF、正方形PBCD,点E在边PD上.设AP=x.