题目内容
13.已知二次函数y=ax2+bx+c(a≠0)的图象经过A(0,3),B(4,0)两点.(1)用仅含字母a的式子表达这个二次函数的解析式.
(2)该二次函数的对称轴不可能是( ),并对你的选择进行证明.
A.x=0 B.x=1 C.x=2 D.x=3
(3)以-a代替(1)中二次函数y的解析式中的a,得到二次函数y′的解析式.
①二次函数y′的图象是否也经过A,B两点?请说明理由.
②当x=t(0≤t≤4)时,求|y-y′|的最大值(用仅含字母a的式子表示).
分析 (1)利用待定系数法即可求得;
(2)根据对称轴公式求得对称轴,即可判断;
(3)①以-a代替(1)中二次函数y的解析式中的a,得到二次函数y′的解析式,然后把A、B两点代入即可验证;
②解|y-y′|得到②|y-y′|=|2a(x-2)2-8a+6|,当x=t时,|y-y′|=|2a(t-2)2-8a+6|,所以当t=2时,有最大值|-8a+6|.
解答 解:(1)将A(0,3),B(4,0)分别代入解析式得
$\left\{\begin{array}{l}c=3\\ 16a+4b+c=0\end{array}\right.$,
解得$\left\{\begin{array}{l}b=-4a-\frac{3}{4}\\ c=3\end{array}\right.$,
故函数解析式为y=ax2-(4a+$\frac{3}{4}$)x+3;
(2)对称轴为x=-$\frac{-(4a+\frac{3}{4})}{2a}$=2+$\frac{3}{8a}$≠2,
故选C.
(3)①y′=-ax2+bx+c,
由(1)可得y′=-ax2-(-4a+$\frac{3}{4}$)x+3,
将x=0代入解析式得,y′=3,故A(0,3)在抛物线上;
将x=4代入解析式得,y′=-16a+16a-3+3=0,故B(4,0)在抛物线上.
②|y-y′|=|ax2-(4a+$\frac{3}{4}$)x+3-[-ax2-(-4a+$\frac{3}{4}$)x+3]|
=|2ax2-8ax+6|
=|2a(x2-4x+4-4)+6|
=|2a(x-2)2-8a+6|
即|y-y′|=|2a(t-2)2-8a+6|,
故|y-y′|最大值为|-8a+6|.
点评 本题考查了待定系数法求二次函数的解析式,二次函数图象上点的坐标特征,二次函数的性质等,待定系数法求解析式是本题的关键.

| A. | 79和74 | B. | 74.5和74 | C. | 74和74.5 | D. | 74和79 |
| A. | -1 | B. | π | C. | 0 | D. | 1 |
| A. | 方程无实数根 | B. | 方程有两个不相等的实数根 | ||
| C. | 方程有两个相等的实数根 | D. | 无法判断 |
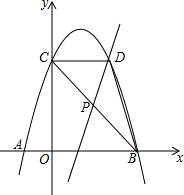 如图,已知抛物线y=ax2+bx+c(a≠0)与x轴交于A、B两点(点A在点B的左边),A(-1,0),B(3,0),与y轴交于点C(0,3)连接BC.
如图,已知抛物线y=ax2+bx+c(a≠0)与x轴交于A、B两点(点A在点B的左边),A(-1,0),B(3,0),与y轴交于点C(0,3)连接BC. 如图,AB∥CD,EF分别交AB、CD与M、N,∠EMB=50°,MG平分∠BMF,MG交CD于G,求∠MGC的度数.
如图,AB∥CD,EF分别交AB、CD与M、N,∠EMB=50°,MG平分∠BMF,MG交CD于G,求∠MGC的度数.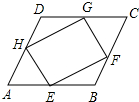 如图,在?ABCD中,E,F,G,H分别是边AB,BC,CD,DA的中点,求证:EFGH是平行四边形.
如图,在?ABCD中,E,F,G,H分别是边AB,BC,CD,DA的中点,求证:EFGH是平行四边形.