��Ŀ����
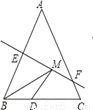
��ͼ������������ABC�ĵױ�BC��Ϊ4�������12����AB�Ĵ�ֱƽ����EF�ֱ�AB��AC�ڵ�E��F������DΪ�ױ�BC���е㣬��MΪ�߶�EF��һ���㣬���BDM���ܳ�����СֵΪ_____________
��ϰ��ϵ�д�
�����Ŀ
�ס������˽��������ϰ����������ͬ�����¸����5�Σ�����ɼ�ͳ�����£�
���л�������λ������ | 7 | 8 | 9 | 10 |
��������Ӧ�����Ĵ��� | 2 | 2 | 0 | 1 |
��������Ӧ�����Ĵ��� | 1 | 3 | 1 | 0 |
��ס�����������ɼ���ƽ�����ֱ��� ����λ��������������
A. 5��5 B. 40��40 C. 8��8 D. 25��24
C ��������������ã� ��=�� ��=. ��ס�����������ɼ���ƽ�����ֱ���8��8. ��ѡC.

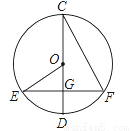
 ����ôn=_____.
����ôn=_____.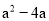 �ֽ���ʽ����ȷ�����( )
�ֽ���ʽ����ȷ�����( )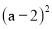 -4
-4 ����С������Ϊ��������
����С������Ϊ��������