题目内容
12. 如图,△ABC沿BC方向平移到△DEF的位置,若EF=5cm,CE=2cm,则AD的长为3cm.
如图,△ABC沿BC方向平移到△DEF的位置,若EF=5cm,CE=2cm,则AD的长为3cm.
分析 先求出CF,再根据平移的性质,对应点的连线的长度等于平移的距离解答.
解答 解:∵EF=5cm,CE=2cm,
∴CF=EF-CE=5-2=3cm,
∵△ABC沿BC方向平移到△DEF的位置,
∴AD=CF=3cm.
故答案为:3.
点评 本题考查平移的基本性质:①平移不改变图形的形状和大小;②经过平移,对应点所连的线段平行且相等,对应线段平行且相等,对应角相等.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
16.下面每个选项中给出了某个变化过程中的两个变量x和y,其中y不是x的函数的选项是( )
| A. | y:正方形的面积;x:这个正方形的周长 | |
| B. | y:某学生的身高;x:这个学生的年龄 | |
| C. | y:圆的面积;x:这个圆的直径 | |
| D. | y:一个数的平方根;x:这个正数 |
7.若a>b,则下列不等式一定成立的是( )
| A. | -1+a<-1+b | B. | $\frac{a}{2}$<$\frac{b}{2}$ | C. | 2-a>2-b | D. | b-a<0 |
17.武汉市在一次扶贫助残活动中,捐款约5180000元,请将5180000元用科学记数法表示为( )
| A. | 0.518×107元 | B. | 5.18×106元 | C. | 51.8×105元 | D. | 518×104元 |
4. 如图,在正方形ABCD外侧作直线DE,点C关于直线DE的对称点为M,连接CM,AM,其中AM交直线DE于点N.若45°<∠CDE<90°,当MN=3,AN=4时,正方形ABCD的边长为( )
如图,在正方形ABCD外侧作直线DE,点C关于直线DE的对称点为M,连接CM,AM,其中AM交直线DE于点N.若45°<∠CDE<90°,当MN=3,AN=4时,正方形ABCD的边长为( )
 如图,在正方形ABCD外侧作直线DE,点C关于直线DE的对称点为M,连接CM,AM,其中AM交直线DE于点N.若45°<∠CDE<90°,当MN=3,AN=4时,正方形ABCD的边长为( )
如图,在正方形ABCD外侧作直线DE,点C关于直线DE的对称点为M,连接CM,AM,其中AM交直线DE于点N.若45°<∠CDE<90°,当MN=3,AN=4时,正方形ABCD的边长为( )| A. | $\sqrt{7}$ | B. | 5 | C. | 5$\sqrt{2}$ | D. | $\frac{5}{2}$$\sqrt{2}$ |
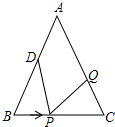 如图,已知△ABC中AB=AC=12厘米,BC=9厘米,点D为AB的中点.
如图,已知△ABC中AB=AC=12厘米,BC=9厘米,点D为AB的中点.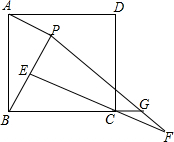 如图,P是矩形ABCD内一点,AP⊥BP于点E,CE⊥BP于点E,BP=EC.
如图,P是矩形ABCD内一点,AP⊥BP于点E,CE⊥BP于点E,BP=EC.