题目内容
6.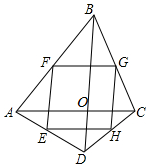 如图,四边形ABCD中,AC⊥BD于O,点E,F,G,H分别为AD,AB,BC,CD的中点.
如图,四边形ABCD中,AC⊥BD于O,点E,F,G,H分别为AD,AB,BC,CD的中点.(1)求证:四边形EFGH是矩形;
(2)若AC=BD,求证:四边形EFGH是正方形.
分析 (1)易证四边形EFGH是平行四边形,再证明有一个角为直角即可证明四边形EFGH是矩形;
(2)由(1)可知EFGH是矩形,再证明其邻边相等即可得到四边形EFGH是正方形.
解答 证明:(1)∵点E,F,G,H分别为AD,AB,BC,CD的中点,
∴EF,GH分别是△ABD和△CBD的中位线,
∴EF∥BD,EF=$\frac{1}{2}$BD,GH∥BD,GH=$\frac{1}{2}$BD,
∴EF=GH,EF∥GH,
∴四边形EFGH是平行四边形,
∵AC⊥BD,
∴EF⊥FG,
∴∠GFE=90°,
∴四边形EFGH是矩形;
(2)∵AC=BD,
∴EF=FG,
又∵四边形EFGH是矩形,
∴四边形EFGH是正方形.
点评 此题考查了中点四边形的性质.学生灵活运用三角形的中位线定理,平行四边形的判断及矩形、正方形的判断进行证明,是一道综合题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,已知AB∥DE,BC∥EF,∠1+∠2+∠3=232°,探索∠2与∠1的度数是定值吗?如果是,请你求出这个定值.
如图,已知AB∥DE,BC∥EF,∠1+∠2+∠3=232°,探索∠2与∠1的度数是定值吗?如果是,请你求出这个定值.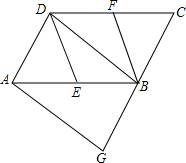 如图,在?ABCD中,E,F分别是边AB,CD的中点,BD是对角线,AG∥BD交GB的延长线于点G.
如图,在?ABCD中,E,F分别是边AB,CD的中点,BD是对角线,AG∥BD交GB的延长线于点G.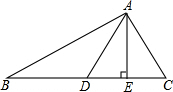 如图,在△ABC中,AD是BC边上的中线,AE⊥BC于E,AB=12,BC=10,AC=8,求DE的长.
如图,在△ABC中,AD是BC边上的中线,AE⊥BC于E,AB=12,BC=10,AC=8,求DE的长. 如图所示,若∠COA=15°,则∠BOD=15°,∠BOC=165°.
如图所示,若∠COA=15°,则∠BOD=15°,∠BOC=165°.