题目内容
1.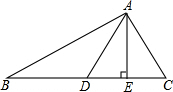 如图,在△ABC中,AD是BC边上的中线,AE⊥BC于E,AB=12,BC=10,AC=8,求DE的长.
如图,在△ABC中,AD是BC边上的中线,AE⊥BC于E,AB=12,BC=10,AC=8,求DE的长.
分析 由AD为BC上的中线,得到BD=CD=$\frac{1}{2}$BC,求出BD与CD的长,设DE=x,得到BE=5+x,CE=5-x,在直角三角形AEC与直角三角形ABE中,分别利用勾股定理表示出AE2,列出关于x的方程,求出方程的解得到x的值,即为DE的长.
解答 解:∵AD为BC边上的中线,
∴BD=CD=$\frac{1}{2}$BC=5,
设DE=x,CE=CD-DE=5-x,
在Rt△AEC中,AE2=AC2-CE2=64-(5-x)2,
在Rt△ABE中,根据勾股定理得:AE2=AB2-BE2=144-(5+x)2,
∴64-(5-x)2=144-(5+x)2,
解得:x=4,
则DE=4.
点评 此题考查了勾股定理,利用了方程的思想,熟练掌握勾股定理是解本题的关键.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
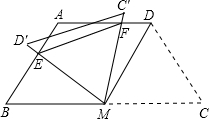 如图,等腰梯形ABCD中,AD∥BC,AD=AB=CD=2,∠C=60°,M是BC的中点.
如图,等腰梯形ABCD中,AD∥BC,AD=AB=CD=2,∠C=60°,M是BC的中点.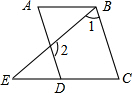 如图,已知∠A=∠C,∠1与∠2互补,
如图,已知∠A=∠C,∠1与∠2互补,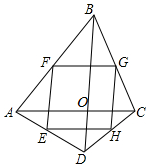 如图,四边形ABCD中,AC⊥BD于O,点E,F,G,H分别为AD,AB,BC,CD的中点.
如图,四边形ABCD中,AC⊥BD于O,点E,F,G,H分别为AD,AB,BC,CD的中点.
 如图,直线a∥b,直线c与a,b相交,若∠2=70°,则∠1=110°.
如图,直线a∥b,直线c与a,b相交,若∠2=70°,则∠1=110°.