题目内容
2.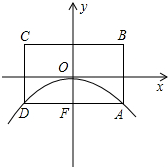 如图所示,矩形ABCD的对称中心和抛物线的顶点均为坐标原点O,点A,D在抛物线上.且AD平行x轴,交y轴于点F,点B的坐标为(2,1).
如图所示,矩形ABCD的对称中心和抛物线的顶点均为坐标原点O,点A,D在抛物线上.且AD平行x轴,交y轴于点F,点B的坐标为(2,1).(1)写出此抛物线的表达式y=-$\frac{1}{4}$x2;
(2)已知直线y=3x+m,当该直线与抛物线只有唯一的公共点时.求此公共点的坐标;
(3)在直角坐标系中,点M(x1,y1),N(x2,y2)之间的距离可以由公式.MN=$\sqrt{({x}_{1}-{x}_{2})^{2}+({y}_{1}-{y}_{2})^{2}}$求出.设点P为抛物线上的动点,过点P作CB 所在直线的垂线,垂足为点E,利用上面公式判断,线段PE与线段PF之间有怎样的大小关系?并说明理由.
分析 (1)由该抛物线的顶点为原点O,设该抛物线的表达式为y=ax2,由点B的坐标结合矩形的性质可得出点A的坐标,再结合点A的坐标利用待定系数法即可求出该抛物线的表达式;
(2)将直线的解析式代入抛物线解析式中,得到关于x的一元二次方程,由二者只有一个交点,结合根的判别式即可得出关于m的一元一次方程,解方程即可求出m的值,再将m的值代入关于x的一元二次方程中,求出x的值,将其代入抛物线解析式即可得出结论;
(3)推断PE=PF,设点P的坐标为(t,-$\frac{1}{4}{t}^{2}$),由此即可得出点E的坐标,利用两点间的距离公式表示出来PE,再结合点A的坐标得出点F的坐标,利用两点间的距离公式表示出PF,比较PE、PF即可得出结论.
解答 解:(1)∵抛物线的顶点为坐标原点O,
∴设该抛物线的表达式为y=ax2.
∵矩形ABCD的对称中心为坐标原点O,且点B的坐标为(2,1),
∴点A的坐标为(2,-1).
∵点A(2,-1)在抛物线y=ax2的图象上,
∴-1=4a,解得:a=-$\frac{1}{4}$,
∴该抛物线的表达式为y=-$\frac{1}{4}$x2.
故答案为:y=-$\frac{1}{4}$x2.
(2)将直线y=3x+m代入到抛物线y=-$\frac{1}{4}$x2中,得:-$\frac{1}{4}$x2=3x+m,
即$\frac{1}{4}$x2+3x+m=0.
∵该直线与抛物线只有唯一的公共点,
∴方程$\frac{1}{4}$x2+3x+m=0有两个相等的实数根,
∴△=32-4×$\frac{1}{4}$m=9-m=0,解得:m=9.
将m=9代入方程$\frac{1}{4}$x2+3x+m=0得:$\frac{1}{4}$x2+3x+9=0,
解得:x1=x2=-6,
将x=-6代入y=-$\frac{1}{4}$x2中,得:y=-$\frac{1}{4}$×(-6)2=-9,
∴该公共点的坐标为(-6,-9).
(3)PE=PF,理由如下:
依照题意做出图形,如图所示.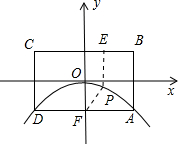
设点P的坐标为(t,-$\frac{1}{4}{t}^{2}$),则点E的坐标为(t,1),
∴PE=$\sqrt{(t-t)^{2}+(-\frac{1}{4}{t}^{2}-1)^{2}}$=$\sqrt{\frac{1}{16}{t}^{4}+\frac{1}{2}{t}^{2}+1}$;
∵点F(0,-1),
∴PF=$\sqrt{(t-0)^{2}+[-\frac{1}{4}{t}^{2}-(-1)]^{2}}$=$\sqrt{\frac{1}{16}{t}^{4}+\frac{1}{2}{t}^{2}+1}$.
∴PE=PF.
点评 本题考查了待定系数法求函数解析式、根的判别式以及两点间的距离公式,解题的关键是:(1)利用待定系数法求出函数解析式;(2)利用根的判别式△=0求出m的值;(3)利用两点间的距离公式求出PE、PF的长度.本题属于中档题,难度不大,解决该题型题目时,将一次函数解析式代入二次函数解析式中,根据两函数相切借助根的判别式△=0求出交点坐标是关键.

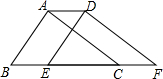 如图,将周长为8的△ABC沿BC方向平移n个单位得到△DEF,得四边形ABFD的周长为10,则n=( )
如图,将周长为8的△ABC沿BC方向平移n个单位得到△DEF,得四边形ABFD的周长为10,则n=( )| A. | 2.5 | B. | 2 | C. | 1 | D. | 0.5 |
| A. | 43 45 | B. | 43 43 | C. | 45 45 | D. | 43 43 |
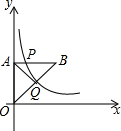 如图,等腰直角三角形OAB的一条直角边在y轴上,点P是边AB上的一个动点,过点P的反比例函数y=$\frac{k}{x}$的图象交斜边OB于点Q,
如图,等腰直角三角形OAB的一条直角边在y轴上,点P是边AB上的一个动点,过点P的反比例函数y=$\frac{k}{x}$的图象交斜边OB于点Q,
 如图,已知梯形ABCD中,AD∥BC,AB=DC,∠D=120°,对角线AC平分∠BCD,且梯形周长为20厘米,求AC的长.
如图,已知梯形ABCD中,AD∥BC,AB=DC,∠D=120°,对角线AC平分∠BCD,且梯形周长为20厘米,求AC的长.