题目内容
11.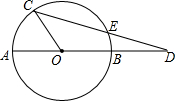 如图所示,AB是⊙0的直径,C是⊙0上一点,∠AOC=54°,CD交⊙0于点E,且DE=0A,求∠D的度数.
如图所示,AB是⊙0的直径,C是⊙0上一点,∠AOC=54°,CD交⊙0于点E,且DE=0A,求∠D的度数.
分析 连接OE,先证明ED=OE,从而可得到∠D=∠EOD=x,然后由三角形的外角的性质和等腰三角形的性质可知∠OCE=∠OEC=2x,最后根据∠EOB+∠AOC=∠OCE+∠OEC求解即可.
解答 解:连接OE.
∵DE=OA,OE=OA,
∴OE=ED.
∴∠D=∠EOD.
设∠D=x,则∠OEC=2x.
∵OC=OE,
∴∠OCE=∠OEC=2x.
∵∠EOB+∠AOC=∠OCE+∠OEC,
∴x+54°=4x.
解得:x=18°.
∴∠D=18°.
点评 本题主要考查的是圆的性质、等腰三角形的性质,根据题意列出关于x的方程是解题的关键.

练习册系列答案
相关题目
1.为了解某校七年级300名学生的视力情况,从中抽出60名学生进行调查,以下说法正确的是( )
| A. | 该校七年级学生是总体 | B. | 该校七年级的每一个学生是个体 | ||
| C. | 抽出的60名学生是样本 | D. | 样本容量是60 |
3.关于x的方程$\frac{m}{x-1}$=1的解为正数,则m的取值范围是( )
| A. | m>-1 | B. | m≠0 | C. | m>1且m≠0 | D. | m>-1且m≠0 |
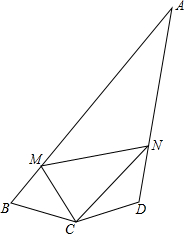 如图,四边形ABCD中,∠B+∠D=180°,∠BCD=150°,CB=CD,M,N为AB、AD上的两个动点,且∠MCN=75°.求证:MN=BM+DN.
如图,四边形ABCD中,∠B+∠D=180°,∠BCD=150°,CB=CD,M,N为AB、AD上的两个动点,且∠MCN=75°.求证:MN=BM+DN.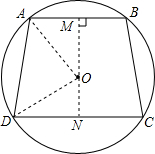 如图,⊙O中,弦AB∥CD,$\widehat{AB}+\widehat{DC}=\widehat{AD}+\widehat{BC}$,AB=10,DC=12,求梯形ABCD的面积.
如图,⊙O中,弦AB∥CD,$\widehat{AB}+\widehat{DC}=\widehat{AD}+\widehat{BC}$,AB=10,DC=12,求梯形ABCD的面积.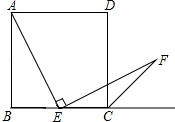 如图,点E是正方形ABCD中BC边上任意一点,以E为端点作EF=AE交∠BCD的外角平分线于F,求证:AE⊥EF.
如图,点E是正方形ABCD中BC边上任意一点,以E为端点作EF=AE交∠BCD的外角平分线于F,求证:AE⊥EF.