题目内容
二次函数y=(x-
)(mx-4m)(其中m>0),下列说法正确的( )
| 1 |
| m |
| A、当x>2时,都有y随着x的增大而增大 | ||
| B、当x<3时,都有y随着x的增大而减小 | ||
C、若当x<n时,都有y随着x的增大而减小,则n≤2+
| ||
D、若当x<n时,都有y随着x的增大而减小,则n≥
|
考点:二次函数的性质
专题:
分析:先求出二次函数的对称轴,再利用此函数图象开口向上,即可判定函数增减性质.
解答:解:y=(x-
)(mx-4m)=mx2-4mx-x+4=m(x-
)2+4-
(其中m>0),
∴二次函数的对称轴为x=2+
,
∵m>0,
∴此函数图象开口向上,
∴当n≤2+
时,y随着x的增大而减小,
故选:C.
| 1 |
| m |
| 4m+1 |
| 2m |
| 16m2+8m+1 |
| 4m2 |
∴二次函数的对称轴为x=2+
| 1 |
| 2m |
∵m>0,
∴此函数图象开口向上,
∴当n≤2+
| 1 |
| 2m |
故选:C.
点评:本题主要考查了二次函数的性质,解题的关键是求出二次函数的对称轴.

练习册系列答案
相关题目
将4个红球、3个白球、2个黑球放入一个不透明的袋子里,从中摸出8个球,恰好红球、白球、黑球都摸到,这个事件是( )
| A、必然事件 | B、不可能事件 |
| C、随机事件 | D、不能确定 |
下列说法中正确的是( )
| A、抛一枚均匀的硬币,出现正面、反面的机会不能确定 |
| B、抛一枚均匀的硬币,出现正面的机会比较大 |
| C、抛一枚均匀的硬币,出现反面的机会比较大 |
| D、抛一枚均匀的硬币,出现正面与反面的机会相等 |
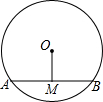 如图,⊙O的弦AB=9,M是AB的中点,且OM为3,则⊙O的半径为
如图,⊙O的弦AB=9,M是AB的中点,且OM为3,则⊙O的半径为 小华和小苗练习射击,两人的成绩如图所示,小华和小苗两人成绩的方差分别为
小华和小苗练习射击,两人的成绩如图所示,小华和小苗两人成绩的方差分别为