题目内容
10.已知⊙O的半径为5,且点O在直线l上,小明用一个三角板学具(∠ABC=90°,AB=BC=8)做数学实验:(1)如图①,若A、B两点在⊙O上滑动,直线BC分别与⊙O、l相交于点D、E.
①求BD的长;②当OE=6时,求BE的长;
(2)如图②,当点B在直线l上,点A在⊙O上,BC与⊙O相切于点P时,则切线长PB=4.

分析 (1)①连接AD,根据90°圆周角所对的弦是直角可知AD是圆O的直径,在△ABD中,依据勾股定理可求得BD的长;
②连接OD,过点O作OF⊥BD,垂足为F.由垂径定理可求得FD、BF的长,然后在△FOE中,依据勾股定理可求得EF的长,从而可求得BE的长.
(2)如图②中,连接PO,并延长交⊙O于点Q,连接AQ,AP,利用△PAQ∽△ABP,得$\frac{AB}{AP}$=$\frac{AP}{PQ}$,求出PA2=80,在RT△PAB中利用勾股定理求出PB即可.
解答 解:(1)①如图1所示:连接AD.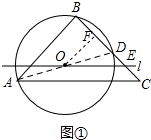
∵∠ABD=90°,
∴AD是圆O的直径.
∴AD=10.
在Rt△ABD中,BD=$\sqrt{A{D}^{2}-A{B}^{2}}$=6.
②如图1所示:过点O作OF⊥BD,垂足为F.
∵OF⊥BD,BD=6,
∴BF=FD=3.
在Rt△ODF中,OF=$\sqrt{O{D}^{2}-F{D}^{2}}$=4.
在Rt△OFE中,EF=$\sqrt{O{E}^{2}-O{F}^{2}}$=2$\sqrt{5}$.
∴BE=FB+EF=3+2$\sqrt{5}$.
如图①′中,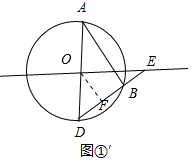
BE=EF-BF=2$\sqrt{5}$-3,
综上所述,BE的值为3+2$\sqrt{5}$或2$\sqrt{5}$-3.
(2)如图②中,连接PO,并延长交⊙O于点Q,连接AQ,AP,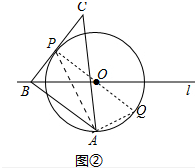
∵BC是⊙O的切线,PQ是直径
∴∠CPO=∠CBA=∠PAQ=90°,
∴PQ∥AB,
∴∠PAB=∠APQ,
∵∠PAQ=∠PBA=90°,
∴△PAQ∽△ABP,
∴$\frac{AB}{AP}$=$\frac{AP}{PQ}$,
∴PA2=80,
在RT△PAB中,PB=$\sqrt{P{A}^{2}-A{B}^{2}}$=$\sqrt{80-64}$=4.
故答案为4.
点评 本题主要考查的是垂径定理、圆周角定理、勾股定理的应用,掌握此类问题的辅助线的作法是解题的关键,学会利用相似三角形的性质解决问题,属于中考常考题型.

 名校课堂系列答案
名校课堂系列答案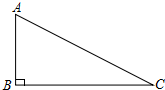 如图,△ABC中,∠B=90°,AB=1,BC=2,则cosA=( )
如图,△ABC中,∠B=90°,AB=1,BC=2,则cosA=( )| A. | $\frac{{\sqrt{5}}}{5}$ | B. | $\frac{{\sqrt{3}}}{3}$ | C. | $\frac{{2\sqrt{5}}}{5}$ | D. | $\frac{1}{2}$ |
 如图,为了绿化荒山,要在山坡上修建一座扬水站,对坡面的绿地进行喷灌,现计划从位于山脚下的机井房A处沿着山坡铺设水泥管道AB,测得斜坡的坡角∠A=27°,出水口的高度BC=225m.
如图,为了绿化荒山,要在山坡上修建一座扬水站,对坡面的绿地进行喷灌,现计划从位于山脚下的机井房A处沿着山坡铺设水泥管道AB,测得斜坡的坡角∠A=27°,出水口的高度BC=225m. 如图,在?ABCD中,E,F分别为边DA,BC的延长线上一点,且AE=CF,连接EF交BD于O.
如图,在?ABCD中,E,F分别为边DA,BC的延长线上一点,且AE=CF,连接EF交BD于O.