题目内容
16.在Rt△ABC中,∠C=90°,AB=10,sin∠B=$\frac{3}{5}$,则BC=( )| A. | 15 | B. | 6 | C. | 9 | D. | 8 |
分析 首先根据正弦函数的定义求得AC的长,然后利用勾股定理求得BC的长.
解答 解:∵sinB=$\frac{AC}{AB}$=$\frac{3}{5}$,
∴AC=AB×$\frac{3}{5}$=6,
∴直角△ABC中,BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=$\sqrt{1{0}^{2}-{6}^{2}}$=8.
故选D.
点评 本题主要考查了解直角三角形、正弦函数的定义;熟练掌握正弦函数的定义是解决问题的关键.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目
6.一个直角三角形两直角边长的比是4:3,斜边长20cm,这个三角形的面积为( )
| A. | 12cm2 | B. | 24cm2 | C. | 48cm2 | D. | 96cm2 |
5.下列个数中,无理数是( )
| A. | 0 | B. | 0.1010010001 | C. | $\sqrt{3}$ | D. | -$\frac{1}{3}$ |
6.一个三角形三遍的长分别为3,5,7,另一个与它相似的三角形的最长边是21,则该三角形的最短边是( )
| A. | 6 | B. | 9 | C. | 10 | D. | 15 |
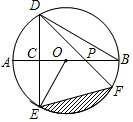 如图,AB是⊙O的直径,弦DE垂直平分半径OA,C为垂足,弦DF与半径OB相交于点P,连结EF、EO,若DE=2$\sqrt{3}$,∠DPA=45°.
如图,AB是⊙O的直径,弦DE垂直平分半径OA,C为垂足,弦DF与半径OB相交于点P,连结EF、EO,若DE=2$\sqrt{3}$,∠DPA=45°.