题目内容
9.一筐梨,先拿走30kg,又拿出余下的70%,这时剩下的梨正好是原来的$\frac{1}{10}$,这筐梨原来多少千克?分析 先先拿走30kg后,又拿出余下的70%,则还剩下余下的1-70%=30%,余下的30%正好是全部的$\frac{1}{10}$,则余下的相当于全部的$\frac{1}{10}$÷30%=$\frac{1}{3}$,所以先拿走30kg相当于全部的1-$\frac{1}{3}$=$\frac{2}{3}$,则这筐梨原来有30$÷\frac{2}{3}$=45kg.
解答 解:30÷[1-$\frac{1}{10}$÷(1-70%)]
=30÷[1-$\frac{1}{10}$÷30%],
=30÷[1-$\frac{1}{3}$],
=30$÷\frac{2}{3}$,
=45(kg).
答:这筐梨原来有45kg.
点评 根据“又拿出余下的70%,这时剩下的梨正好是原来的$\frac{1}{10}$”求出余下部分占总数的分率是完成本题的关键.

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
20.单项式-xy2( )
| A. | 系数是0,次数是3 | B. | 系数是-1,次数是2 | ||
| C. | 系数是1,次数是2 | D. | 系数是-1,次数是3 |
18.在一次献爱心捐赠活动中,某班45名同学捐款金额统计如下:
在这次活动中,该班同学捐款金额的众数和中位数分别是( )
| 金额(元) | 20 | 30 | 35 | 50 | 100 |
| 学生数(人) | 10 | 13 | 5 | 15 | 2 |
| A. | 15,13 | B. | 15,30 | C. | 50,30 | D. | 50,35 |
 如图,AB∥CD,AC⊥CE,∠BAE=3∠DCE,∠E=54°,求∠BAC的度数.
如图,AB∥CD,AC⊥CE,∠BAE=3∠DCE,∠E=54°,求∠BAC的度数.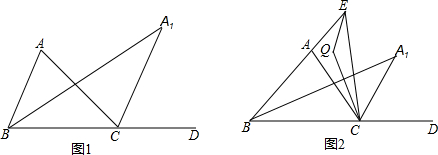
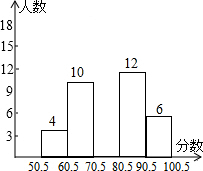 某班数学期末考试后,班主任将所得的成绩(分数取整数)进行整理分成5组,并绘成频数分布直方图(如图),已知70.5~80.5分数段的频率为0.36,请结合直方图提供的信息,解答以下问题:
某班数学期末考试后,班主任将所得的成绩(分数取整数)进行整理分成5组,并绘成频数分布直方图(如图),已知70.5~80.5分数段的频率为0.36,请结合直方图提供的信息,解答以下问题: 如图,己知AB=8,以AB为斜边作Rt△ABC,∠ACB=90°,过点C作AB的平行线,再过点A作AB的垂线,使两线相交于点D.设AC=x,DC=y;则(x-y)的最大值是2.
如图,己知AB=8,以AB为斜边作Rt△ABC,∠ACB=90°,过点C作AB的平行线,再过点A作AB的垂线,使两线相交于点D.设AC=x,DC=y;则(x-y)的最大值是2.