题目内容
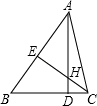
如图,在△ABC中,AD⊥BC,CE⊥AB,垂足分别为D、E,AD、CE交于点H,已知EH=EB=3,AE=4,则CH的长是__________.
1.
【考点】全等三角形的判定与性质.
【专题】几何图形问题.
【分析】根据AD⊥BC,CE⊥AB,得出∠ADB=∠AEH=90°,再根据∠BAD=∠BCE,利用AAS得到△HEA≌△BEC,由全等三角形的对应边相等得到AE=EC,由HC=EC﹣EH代入计算即可.
【解答】解:∵AD⊥BC,CE⊥AB,
∴∠ADB=∠AEH=90°,
∵∠AHE=∠CHD,
∴∠BAD=∠BCE,
∵在△HEA和△BEC中,
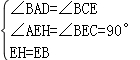 ,
,
∴△HEA≌△BEC(AAS),
∴AE=EC=4,
则CH=EC﹣EH=AE﹣EH=4﹣3=1.
故答案为:1.
【点评】此题考查了全等三角形的判定与性质,用到的知识点是全等三角形的判定与性质,解题的关键是找出图中的全等三角形,并进行证明.

练习册系列答案
相关题目
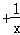 =c
=c 的解是x1=c,x2=
的解是x1=c,x2= ;
;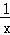 =c﹣
=c﹣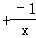 =c
=c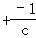 的解是x1=c,x2=﹣
的解是x1=c,x2=﹣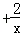 =c
=c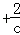 的解是x1=c,x2=
的解是x1=c,x2=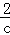 ;
;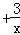 =c
=c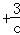 的解是x1=c,x2=
的解是x1=c,x2=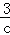 ;
;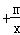 =c
=c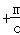 (m≠0)的解,并验证你的结论.
(m≠0)的解,并验证你的结论.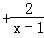 =a
=a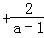 .
.
 ,3
,3
 作图痕迹)
作图痕迹)
