题目内容
7.从-2,-1,0,1,2,4这六个数中,任取一个数作为a的值,恰好使得关于x、y的二元一次方程组$\left\{\begin{array}{l}{x-y=a}\\{x+y=2}\end{array}\right.$有整数解,且函数y=ax2+4x+2与x轴有公共点的概率是$\frac{1}{2}$.分析 从6个数中找到使得关于x、y的二元一次方程组$\left\{\begin{array}{l}{x-y=a}\\{x+y=2}\end{array}\right.$有整数解,且函数y=ax2+4x+2与x轴有公共点的a的个数后利用概率公式求解即可.
解答 解:能使得使得关于x、y的二元一次方程组$\left\{\begin{array}{l}{x-y=a}\\{x+y=2}\end{array}\right.$有整数解的a的值有-2,0,2,4共四个数,
∵y=ax2+4x+2与x轴有公共点,
∴b2-4ac=16-8a≥0,
解得:a≤2,
∴使得关于x、y的二元一次方程组$\left\{\begin{array}{l}{x-y=a}\\{x+y=2}\end{array}\right.$有整数解,且函数y=ax2+4x+2与x轴有公共点的a的值有-2,0,2共3个,
∴P(使得关于x、y的二元一次方程组$\left\{\begin{array}{l}{x-y=a}\\{x+y=2}\end{array}\right.$有整数解,且函数y=ax2+4x+2与x轴有公共点)=$\frac{3}{6}$=$\frac{1}{2}$,
故答案为:$\frac{1}{2}$.
点评 此题考查了概率公式的应用以及根的判别式与二次函数的性质.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
2.下列说法错误的是( )
| A. | 把4个球放入三个抽屉中,其中一个抽屉中至少有2个球是必然事件 | |
| B. | 数据1、2、2、3的平均数是2 | |
| C. | 数据5、2、-3、0的极差是8 | |
| D. | 如果某种游戏活动的中奖率为40%,那么参加这种活动10次一定有4次中奖 |
19.徐州属于全国40个重度缺水的城市之一,徐州水资源总量为47.9亿m3.请将47.9亿用科学记数法表示出来( )
| A. | 4.79×107 | B. | 4.79×108 | C. | 4.79×109 | D. | 4.79×1010 |
17.若关于x的不等式(2-m)x≤m-2的解集为x≥-1,则m应满足的条件是( )
| A. | m>0 | B. | m<2 | C. | m≥2 | D. | m>2 |
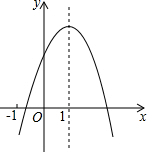 已知二次函数y=ax2+bx+c的图象如图所示,下列结论中,正确的结论的个数( )
已知二次函数y=ax2+bx+c的图象如图所示,下列结论中,正确的结论的个数( )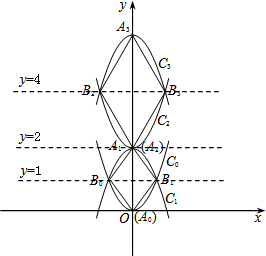 如图,已知抛物线C0:y=x2,顶点记作A0.首先我们将抛物线C0关于直线y=1对称翻折过去得到抛物线C1称为第一次操作,再将抛物线C1关于直线y=2对称翻折过去得到抛物线C2称为第二次操作,…,将抛物线Cn-1关于直线y=2n-1对称翻折过去得到抛物线Cn(顶点记作An)称为第n此操作(n=1,2,3…),….设抛物线C0与抛物线C1交于两点B0与B1,顺次连接A0、B0、A1、B1四个点得到四边形A0B0A1B1,抛物线C2与抛物线C3交于两点B2与B3,顺次连接A2、B2、A3、B3四个点得到四边形A2B2A3B3,…,抛物线Ck-1与抛物线Ck交于两点Bk-1与Bk,顺次连接Ak-1、Bk-1、Ak、Bk四个点得到四边形Ak-1Bk-1AkBk(k=1,3,5…),….
如图,已知抛物线C0:y=x2,顶点记作A0.首先我们将抛物线C0关于直线y=1对称翻折过去得到抛物线C1称为第一次操作,再将抛物线C1关于直线y=2对称翻折过去得到抛物线C2称为第二次操作,…,将抛物线Cn-1关于直线y=2n-1对称翻折过去得到抛物线Cn(顶点记作An)称为第n此操作(n=1,2,3…),….设抛物线C0与抛物线C1交于两点B0与B1,顺次连接A0、B0、A1、B1四个点得到四边形A0B0A1B1,抛物线C2与抛物线C3交于两点B2与B3,顺次连接A2、B2、A3、B3四个点得到四边形A2B2A3B3,…,抛物线Ck-1与抛物线Ck交于两点Bk-1与Bk,顺次连接Ak-1、Bk-1、Ak、Bk四个点得到四边形Ak-1Bk-1AkBk(k=1,3,5…),….