题目内容
12. 如图所示,在△ABC中,∠BAC=90°,AB⊥AC,AB=3,BC=5,EF垂直平分BC,点P为直线EF上的任一点,则AP+BP的最小值是4.
如图所示,在△ABC中,∠BAC=90°,AB⊥AC,AB=3,BC=5,EF垂直平分BC,点P为直线EF上的任一点,则AP+BP的最小值是4.
分析 根据题意知点B关于直线EF的对称点为点C,故当点P与点D重合时,AP+BP的最小值,求出AC长度即可.
解答  解:∵EF垂直平分BC,
解:∵EF垂直平分BC,
∴B、C关于EF对称,
AC交EF于D,
∴当P和D重合时,AP+BP的值最小,最小值等于AC的长,
由勾股定理得:AC=$\sqrt{B{C}^{2}-A{B}^{2}}$=4.
故答案为:4.
点评 本题考查了勾股定理,轴对称-最短路线问题的应用,解此题的关键是找出P的位置.

练习册系列答案
相关题目
2.下列各式中,是完全平方式的是( )
| A. | m2-4m-1 | B. | x2-2x-1 | C. | x2+2x+$\frac{1}{4}$ | D. | $\frac{1}{4}$b2-ab+a2 |
7.下列说法正确的是( )
| A. | 掷一枚均匀的骰子,骰子停止转动后,6点朝上是必然事件 | |
| B. | 甲、乙两人在相同条件下各射击10次,他们的成绩平均数相同,方差分别是S甲2=0.4,S乙2=0.6,则甲的射击成绩较稳定 | |
| C. | “明天降雨的概率为$\frac{1}{2}$”,表示明天有半天都在降雨 | |
| D. | “彩票中奖的概率为1%”,表示买100张彩票一定会中奖 |
 如图,在山顶上有一座电视塔,在塔顶B处,测得地面上一点A的俯角α=60°,在塔底C处测得的俯角β=45°,已知BC=60m,求山高CD(精确到1m,$\sqrt{3}$≈1.732)
如图,在山顶上有一座电视塔,在塔顶B处,测得地面上一点A的俯角α=60°,在塔底C处测得的俯角β=45°,已知BC=60m,求山高CD(精确到1m,$\sqrt{3}$≈1.732) 如图,已知E、F分别为平行四边形ABCD的对边AD、BC上的点,且DE=BF,EM⊥AC于M,FN⊥AC于N,EF交AC于点O,求证:
如图,已知E、F分别为平行四边形ABCD的对边AD、BC上的点,且DE=BF,EM⊥AC于M,FN⊥AC于N,EF交AC于点O,求证: 如图,△ABC的顶点均在格点上,利用网格线在图中找一点O,使得OA=OB=OC.
如图,△ABC的顶点均在格点上,利用网格线在图中找一点O,使得OA=OB=OC.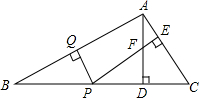 如图,△ABC中.∠B=22.5°,AB的垂直平分线交AB于点Q,交BC于点P,PE⊥AC于点E,AD⊥BC于点D,AD交PE于点F.求证:DF=DC.
如图,△ABC中.∠B=22.5°,AB的垂直平分线交AB于点Q,交BC于点P,PE⊥AC于点E,AD⊥BC于点D,AD交PE于点F.求证:DF=DC.