题目内容
9.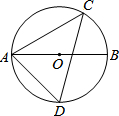 如图,AB为⊙O的直径,点C在⊙O上,且∠CAB=30°,点D为弧$\widehat{AB}$的中点,AC=4$\sqrt{3}$.求AD的长.
如图,AB为⊙O的直径,点C在⊙O上,且∠CAB=30°,点D为弧$\widehat{AB}$的中点,AC=4$\sqrt{3}$.求AD的长.
分析 连接BC、BD,根据余弦的定义求出AB,根据等腰直角三角形的性质求出AD即可.
解答 解: 连接BC、BD,
连接BC、BD,
∵AB为⊙O的直径,
∴∠ACB=90°,又∠CAB=30°,
∴AB=$\frac{AC}{cos30°}$=8,
∵点D为弧$\widehat{AB}$的中点,
∴AD=BD=4$\sqrt{2}$.
点评 本题考查的是圆周角定理、锐角三角函数的定义,掌握直径所对的圆周角是直角是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14.在下面的图形中,形状相似的一组是( )
| A. | 任意两个等腰三角形 | B. | 任意两个矩形 | ||
| C. | 任意两个等边三角形 | D. | 任意两个菱形 |
18.下列运算正确的是( )
| A. | 2a+3b=5ab | B. | a3•a3•a3=3a3 | C. | (ab2)3=a3b6 | D. | (a+b)2=a2+b2 |
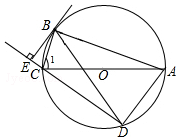 如图,⊙O是△ABC的外接圆,AC为直径,弦BD=BA,过点B作⊙O的切线交DC的延长线于点E.
如图,⊙O是△ABC的外接圆,AC为直径,弦BD=BA,过点B作⊙O的切线交DC的延长线于点E. 如图的方格纸中,每个小正方形的边长均为1,每个小正方形的顶点叫做格点.
如图的方格纸中,每个小正方形的边长均为1,每个小正方形的顶点叫做格点.