题目内容
1. 如图的方格纸中,每个小正方形的边长均为1,每个小正方形的顶点叫做格点.
如图的方格纸中,每个小正方形的边长均为1,每个小正方形的顶点叫做格点.(1)在图中画出以AB为边的钝角三角形ABC,使点C在格点上,并且在直线AB的上方,满足tan∠BAC=$\frac{1}{3}$,且△ABC的面积为9;
(2)以AC为斜边画Rt△ACD,使D点在AC上方,且满足tan∠ACD=2
;
(3)直接写出线段CD的长.
分析 (1)根据钝角三角形ABC,满足tan∠BAC=$\frac{1}{3}$,且△ABC的面积为9进行作图;
(2)根据Rt△ACD,满足tan∠ACD=2进行画图即可;
(3)根据勾股定理求得线段CD的长.
解答 解:(1)如图所示,△ABC即为所求;
(2)如图所示,△ADC即为所求;
(3)如图所示,CD=$\sqrt{{3}^{2}+{3}^{2}}$=$3\sqrt{2}$.
点评 本题主要考查了勾股定理的应用,首先要理解题意,弄清问题中对所作图形的要求,结合对应几何图形的性质和基本作图的方法作图.

练习册系列答案
相关题目
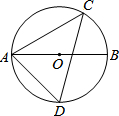 如图,AB为⊙O的直径,点C在⊙O上,且∠CAB=30°,点D为弧$\widehat{AB}$的中点,AC=4$\sqrt{3}$.求AD的长.
如图,AB为⊙O的直径,点C在⊙O上,且∠CAB=30°,点D为弧$\widehat{AB}$的中点,AC=4$\sqrt{3}$.求AD的长. 如图,AD是∠EAC的平分线,AD∥BC,∠B=40°,则∠DAC的度数为40°.
如图,AD是∠EAC的平分线,AD∥BC,∠B=40°,则∠DAC的度数为40°.