题目内容
19.下列方程:(x+1)(x-2)=3,x2+y+4=0,(x-1)2-x(x+1)=x,x+$\frac{1}{x}$=0,$\sqrt{{x}^{2}+1}$-2x=4,$\frac{1}{2}$(x2+3)=$\sqrt{5}$,其中是一元二次方程的有( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
分析 根据一元二次方程的定义:只含有一个未知数,并且未知数的最高次数是2的整式方程叫一元二次方程进行分析即可.
解答 解:(x+1)(x-2)=3,$\frac{1}{2}$(x2+3)=$\sqrt{5}$是一元二次方程,共2个,
故选:A.
点评 此题主要考查了一元二次方程的定义,判断一个方程是否是一元二次方程应注意抓住5个方面:“化简后”;“一个未知数”;“未知数的最高次数是2”;“二次项的系数不等于0”;“整式方程”.

练习册系列答案
相关题目
4.要使(x2+ax+5)(-6x3)的展开式中不含x4项,则a应等于( )
| A. | 1 | B. | -1 | C. | $\frac{1}{6}$ | D. | 0 |
9.在-2,0,-4,π这四个数中,最小的数是( )
| A. | -2 | B. | 0 | C. | -4 | D. | π |
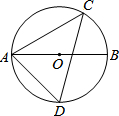 如图,AB为⊙O的直径,点C在⊙O上,且∠CAB=30°,点D为弧$\widehat{AB}$的中点,AC=4$\sqrt{3}$.求AD的长.
如图,AB为⊙O的直径,点C在⊙O上,且∠CAB=30°,点D为弧$\widehat{AB}$的中点,AC=4$\sqrt{3}$.求AD的长.