题目内容
 如图,将一块直角三角板OAB放在平面直角坐标系中,B(2,0),∠AOB=60°,点A在第一象限,过点A的双曲线为
如图,将一块直角三角板OAB放在平面直角坐标系中,B(2,0),∠AOB=60°,点A在第一象限,过点A的双曲线为 .在x轴上取一点P,过点P作直线OA的垂线l,以直线l为对称轴,线段OB经轴对称变换后的像是O′B′.当点O′与点A重合时,点P的坐标是________.
.在x轴上取一点P,过点P作直线OA的垂线l,以直线l为对称轴,线段OB经轴对称变换后的像是O′B′.当点O′与点A重合时,点P的坐标是________.
(4,0)
分析:根据轴对称变换的性质得到当点O′与点A重合时,直线l垂直平分OA,则PA=PB,由B(2,0),∠AOB=60°,根据含30度的直角三角形三边的关系得到AB= OB=2
OB=2 ,然后设P点坐标为(x,0),则PA=PB=x,PB=x-2,在Rt△PAB中利用勾股定理得到x2=(x-2)2+(2
,然后设P点坐标为(x,0),则PA=PB=x,PB=x-2,在Rt△PAB中利用勾股定理得到x2=(x-2)2+(2 )2,解得x=4,即可确定P点坐标.
)2,解得x=4,即可确定P点坐标.
解答:点O′与点A重合时,直线l垂直平分OA,如图,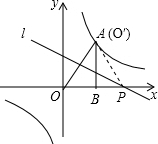
连PA,则PA=PO,
∵B(2,0),∠AOB=60°,
∴OB=2,
∴AB= OB=2
OB=2 ,
,
设P点坐标为(x,0),则PA=PO=x,PB=x-2,
在Rt△PAB中,PA2=PB2+AB2,即x2=(x-2)2+(2 )2,解得x=4,
)2,解得x=4,
∴P点坐标为(4,0).
故答案为(4,0).
点评:本题考查了轴对称变换的性质:轴对称变换不改变原图形的形状和大小,即变换后图形与原图形全等.也考查了勾股定理以及含30度的直角三角形三边的关系.
分析:根据轴对称变换的性质得到当点O′与点A重合时,直线l垂直平分OA,则PA=PB,由B(2,0),∠AOB=60°,根据含30度的直角三角形三边的关系得到AB=
 OB=2
OB=2 ,然后设P点坐标为(x,0),则PA=PB=x,PB=x-2,在Rt△PAB中利用勾股定理得到x2=(x-2)2+(2
,然后设P点坐标为(x,0),则PA=PB=x,PB=x-2,在Rt△PAB中利用勾股定理得到x2=(x-2)2+(2 )2,解得x=4,即可确定P点坐标.
)2,解得x=4,即可确定P点坐标.解答:点O′与点A重合时,直线l垂直平分OA,如图,

连PA,则PA=PO,
∵B(2,0),∠AOB=60°,
∴OB=2,
∴AB=
 OB=2
OB=2 ,
,设P点坐标为(x,0),则PA=PO=x,PB=x-2,
在Rt△PAB中,PA2=PB2+AB2,即x2=(x-2)2+(2
 )2,解得x=4,
)2,解得x=4,∴P点坐标为(4,0).
故答案为(4,0).
点评:本题考查了轴对称变换的性质:轴对称变换不改变原图形的形状和大小,即变换后图形与原图形全等.也考查了勾股定理以及含30度的直角三角形三边的关系.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
 如图,将一块直角三角板OAB放在平面直角坐标系中,B(2,0),∠AOB=60°,点A在第一象限,过点A的双曲线为
如图,将一块直角三角板OAB放在平面直角坐标系中,B(2,0),∠AOB=60°,点A在第一象限,过点A的双曲线为 如图,将一块直角三角板OAB放在平面直角坐标系中,B(2,0),∠AOB=60°,点A在第一象限,过点A的双曲线为
如图,将一块直角三角板OAB放在平面直角坐标系中,B(2,0),∠AOB=60°,点A在第一象限,过点A的双曲线为 如图,将一块直角三角板OAB放在平面直角坐标系中,B(2,0),∠AOB=60°,点A在第一象限,过点A的双曲线为
如图,将一块直角三角板OAB放在平面直角坐标系中,B(2,0),∠AOB=60°,点A在第一象限,过点A的双曲线为 (2012•潮阳区模拟)如图,将一块直角三角板ABC和半圆形量角器按图中方式叠放,其中∠A=30°,半圆O的直径MN与直线AC重叠,且切AB于点E,交BC于点F,若测得OM=6cm,∠AOF=120°,求图中阴影部分的面积.(结果可保留π)
(2012•潮阳区模拟)如图,将一块直角三角板ABC和半圆形量角器按图中方式叠放,其中∠A=30°,半圆O的直径MN与直线AC重叠,且切AB于点E,交BC于点F,若测得OM=6cm,∠AOF=120°,求图中阴影部分的面积.(结果可保留π) 如图,将一块直角三角板放置在圆上,使30°角的顶点落在圆上,角的两边与⊙O相交于A、B两点,OA=6cm,则弦AB=
如图,将一块直角三角板放置在圆上,使30°角的顶点落在圆上,角的两边与⊙O相交于A、B两点,OA=6cm,则弦AB=