题目内容
 如图,将一块直角三角板OAB放在平面直角坐标系中,B(2,0),∠AOB=60°,点A在第一象限,过点A的双曲线为y=
如图,将一块直角三角板OAB放在平面直角坐标系中,B(2,0),∠AOB=60°,点A在第一象限,过点A的双曲线为y=| k | x |
(1)当点O′与点A重合时,点P的坐标是
(2)设P(t,0),当O′B′与双曲线有交点时,t的取值范围是
分析:(1)当点O?与点A重合时,即点O与点A重合,进一步解直角三角形AOB,利用轴对称的现在解答即可;
(2)分别求出O′和B′在双曲线上时,P的坐标即可.
(2)分别求出O′和B′在双曲线上时,P的坐标即可.
解答: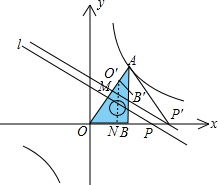 解:(1)当点O?与点A重合时
解:(1)当点O?与点A重合时
∵∠AOB=60°,过点P作直线OA的垂线l,以直线l为对称轴,线段OB经轴对称变换后是O?B?.
AP=OP,
∴△AOP′是等边三角形,
∵B(2,0),
∴BO=BP′=2,
∴点P的坐标是(4,0),
故答案为:(4,0).
(2)由(1)知,当P的坐标是(4,0)时,直线O?B?与双曲线有交点O′,
当B′在双曲线上时,作B′C⊥OP于C,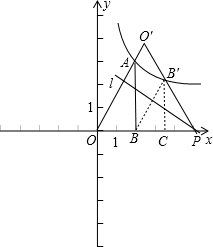
∵BP=B′P,∠B′BP=60°,
∴△BB′P是等边三角形,
∴BP=B′P=t-2,
∴CP=
(t-2),B′C=
(t-2),
∴OC=OP-CP=
t+1,
∴B′的坐标是(
t+1,
(t-2)),
∵∠ABO=90°,∠AOB=60°,OB=2,
∴OA=4,AB=2
,
∴A(2,2
),
∵A和B′都在双曲线上,
∴(
t+1)•
(t-2))=2×2
,
解得:t=±2
,
∴t的取值范围是4≤t≤2
或-2
≤t≤-4.
故答案为:4≤t≤2
或-2
≤t≤-4.
 解:(1)当点O?与点A重合时
解:(1)当点O?与点A重合时∵∠AOB=60°,过点P作直线OA的垂线l,以直线l为对称轴,线段OB经轴对称变换后是O?B?.
AP=OP,
∴△AOP′是等边三角形,
∵B(2,0),
∴BO=BP′=2,
∴点P的坐标是(4,0),
故答案为:(4,0).
(2)由(1)知,当P的坐标是(4,0)时,直线O?B?与双曲线有交点O′,
当B′在双曲线上时,作B′C⊥OP于C,

∵BP=B′P,∠B′BP=60°,
∴△BB′P是等边三角形,
∴BP=B′P=t-2,
∴CP=
| 1 |
| 2 |
| ||
| 2 |
∴OC=OP-CP=
| 1 |
| 2 |
∴B′的坐标是(
| 1 |
| 2 |
| ||
| 2 |
∵∠ABO=90°,∠AOB=60°,OB=2,
∴OA=4,AB=2
| 3 |
∴A(2,2
| 3 |
∵A和B′都在双曲线上,
∴(
| 1 |
| 2 |
| ||
| 2 |
| 3 |
解得:t=±2
| 5 |
∴t的取值范围是4≤t≤2
| 5 |
| 5 |
故答案为:4≤t≤2
| 5 |
| 5 |
点评:本题主要考查对用待定系数法求一次函数、反比例函数的解析式,勾股定理,解二元一次方程组,解不等式,含30度角的直角三角形的性质,三角形的内角和定理,根的判别式等知识点的理解和掌握,能综合运用这些性质进行计算是解此题的关键,此题是一个拔高的题目,有一定的难度.

练习册系列答案
相关题目
 如图,将一块直角三角板OAB放在平面直角坐标系中,B(2,0),∠AOB=60°,点A在第一象限,过点A的双曲线为
如图,将一块直角三角板OAB放在平面直角坐标系中,B(2,0),∠AOB=60°,点A在第一象限,过点A的双曲线为 如图,将一块直角三角板OAB放在平面直角坐标系中,B(2,0),∠AOB=60°,点A在第一象限,过点A的双曲线为
如图,将一块直角三角板OAB放在平面直角坐标系中,B(2,0),∠AOB=60°,点A在第一象限,过点A的双曲线为 (2012•潮阳区模拟)如图,将一块直角三角板ABC和半圆形量角器按图中方式叠放,其中∠A=30°,半圆O的直径MN与直线AC重叠,且切AB于点E,交BC于点F,若测得OM=6cm,∠AOF=120°,求图中阴影部分的面积.(结果可保留π)
(2012•潮阳区模拟)如图,将一块直角三角板ABC和半圆形量角器按图中方式叠放,其中∠A=30°,半圆O的直径MN与直线AC重叠,且切AB于点E,交BC于点F,若测得OM=6cm,∠AOF=120°,求图中阴影部分的面积.(结果可保留π) 如图,将一块直角三角板放置在圆上,使30°角的顶点落在圆上,角的两边与⊙O相交于A、B两点,OA=6cm,则弦AB=
如图,将一块直角三角板放置在圆上,使30°角的顶点落在圆上,角的两边与⊙O相交于A、B两点,OA=6cm,则弦AB=