题目内容
4.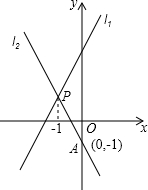 如图,直线l1与l2相交于点P,l1的解析式为y=2x+3,点P的横坐标为-1,且l2交y轴于点A(0,-1).
如图,直线l1与l2相交于点P,l1的解析式为y=2x+3,点P的横坐标为-1,且l2交y轴于点A(0,-1).(1)求直线l2的函数解析式;
(2)求这两条直线与y轴围成的图形的面积.
分析 (1)根据l1的解析式求出P点的坐标,再设出l2的解析式,利用待定系数法就可以求出l2的解析式.
(2)设l1交y轴于点B,求出B点坐标,得到AB的长,再利用P点的横坐标就可以求出△PAB的面积.
解答 解:(1)设点P坐标为(-1,y),
代入y=2x+3,得y=1,
则点P(-1,1).
设直线l2的函数表达式为y=kx+b,
把P(-1,1)、A(0,-1)分别代入y=kx+b,
得1=-k+b,-1=b,
解得k=-2,b=-1.
所以直线l2的函数表达式为y=-2x-1; (2)设l1交y轴于点B,如图.
(2)设l1交y轴于点B,如图.
∵l1的解析式为y=2x+3,
∴x=0时,y=3,
∴B(0,3),
∵A(0,-1),
∴AB=4,
∵P(-1,1),
S△PAB=$\frac{1}{2}$×4×1=2.
点评 本题考查待定系数法求直线的解析式,点的坐标,直线的交点坐标以及三角形的面积.求三角形的面积时找出高和底边长即可.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
12. 如图,点O是矩形ABCD的中心,E是AB上的点,沿CE折叠后,点B恰好与点O重合,若BC=3,则折痕CE的长为( )
如图,点O是矩形ABCD的中心,E是AB上的点,沿CE折叠后,点B恰好与点O重合,若BC=3,则折痕CE的长为( )
 如图,点O是矩形ABCD的中心,E是AB上的点,沿CE折叠后,点B恰好与点O重合,若BC=3,则折痕CE的长为( )
如图,点O是矩形ABCD的中心,E是AB上的点,沿CE折叠后,点B恰好与点O重合,若BC=3,则折痕CE的长为( )| A. | 2$\sqrt{3}$ | B. | $\frac{3\sqrt{3}}{2}$ | C. | $\sqrt{3}$ | D. | 6 |
13.正比例函数y=-2x的大致图象是( )
| A. |  | B. |  | C. |  | D. |  |
14. 如图,在?ABCD中,点在AD边上,EF∥CD,交对角线BD于点F,则下列结论中错误的是( )
如图,在?ABCD中,点在AD边上,EF∥CD,交对角线BD于点F,则下列结论中错误的是( )
 如图,在?ABCD中,点在AD边上,EF∥CD,交对角线BD于点F,则下列结论中错误的是( )
如图,在?ABCD中,点在AD边上,EF∥CD,交对角线BD于点F,则下列结论中错误的是( )| A. | $\frac{DE}{AE}$=$\frac{DF}{BF}$ | B. | $\frac{EF}{AB}$=$\frac{DF}{DB}$ | C. | $\frac{EF}{CD}$=$\frac{DF}{BF}$ | D. | $\frac{EF}{CD}$=$\frac{DF}{DB}$ |
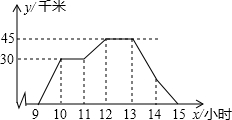 A、B两地路程为45千米,图中折线表示骑车人离A地的路程y与时间x的函数关系,一辆客车10:30从A地出发,沿与骑车人相同的路线以45千米/时的速度往返于A、B两地之间(往返中不停留),以下结论正确的个数有( )
A、B两地路程为45千米,图中折线表示骑车人离A地的路程y与时间x的函数关系,一辆客车10:30从A地出发,沿与骑车人相同的路线以45千米/时的速度往返于A、B两地之间(往返中不停留),以下结论正确的个数有( )