题目内容
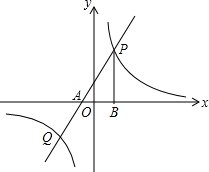 如图,经过点A(-2,0)的一次函数y=ax+b(a≠0)与反比例函数y=
如图,经过点A(-2,0)的一次函数y=ax+b(a≠0)与反比例函数y=| k |
| x |
| 3 |
| 2 |
(1)求反比例函数和一次函数的解析式;
(2)若点Q的坐标是Q(m,-6),连接OQ,求△COQ的面积.
考点:反比例函数与一次函数的交点问题
专题:计算题
分析:(1)由A与B坐标求出AB的长,在三角形PAB中,利用锐角三角函数定义求出BP的长,确定出P的坐标,将P坐标代入反比例解析式中求出k的值,确定出反比例解析式,将A与P坐标代入一次函数解析式中求出a与b的值,确定出一次函数解析式;
(2)将Q坐标代入反比例解析式中求出m的值,确定出Q坐标,对于一次函数,令x=0求出y的值,求出C的坐标,求出三角形COQ的面积即可.
(2)将Q坐标代入反比例解析式中求出m的值,确定出Q坐标,对于一次函数,令x=0求出y的值,求出C的坐标,求出三角形COQ的面积即可.
解答: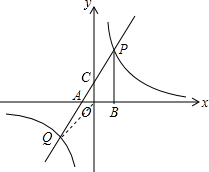 解:(1)∵A(-2,0),B(4,0),
解:(1)∵A(-2,0),B(4,0),
∴AB=6,
∵tan∠PAB=
,
∴
=
,解得:BP=9,
∴P(4,9),
把P(4,9)代入y=
中,得 k=36.
∴反比例函数的解析式为 y=
,
将A(-2,0),P(4,9)代入y=ax+b中,得
,
解得:
,
∴一次函数的解析式为y=
x+3;
(2)由(1)得Q(-6,-6),
对于一次函数y=
x+3,令x=0求出y=3,即C(0,3),
则△COQ的面积为S=
×3×6=9.
 解:(1)∵A(-2,0),B(4,0),
解:(1)∵A(-2,0),B(4,0),∴AB=6,
∵tan∠PAB=
| 3 |
| 2 |
∴
| BP |
| 6 |
| 3 |
| 2 |
∴P(4,9),
把P(4,9)代入y=
| k |
| x |
∴反比例函数的解析式为 y=
| 36 |
| x |
将A(-2,0),P(4,9)代入y=ax+b中,得
|
解得:
|
∴一次函数的解析式为y=
| 3 |
| 2 |
(2)由(1)得Q(-6,-6),
对于一次函数y=
| 3 |
| 2 |
则△COQ的面积为S=
| 1 |
| 2 |
点评:此题考查了反比例函数与一次函数的交点问题,涉及的知识有:待定系数法求函数解析式,坐标与图形性质,锐角三角函数定义,熟练掌握待定系数法是解本题的关键.

练习册系列答案
相关题目
在△ABC中,∠A是钝角,H是垂心,AH=BC,则∠BHC=( )
| A、30° | B、45° |
| C、60° | D、75° |
下列运算正确的是( )
A、
| ||||
B、2+
| ||||
| C、(x+y)2=x2+y2 | ||||
| D、(-ab)2=a2b2 |
如图所示下列几何体中,俯视图形状相同的是( )


| A、①④ | B、②③ |
| C、①②④ | D、②③④ |
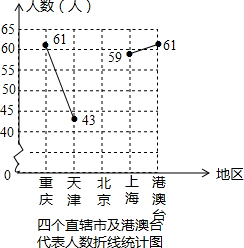 第十二届全国人大代表选举的基本原则是:城乡同比选举,实现人人平等、地区平等、民族平等.据新华网2月28日公布,全国5个少数民族自治区的人大代表如下:
第十二届全国人大代表选举的基本原则是:城乡同比选举,实现人人平等、地区平等、民族平等.据新华网2月28日公布,全国5个少数民族自治区的人大代表如下: 商城义乌江的两岸绿树葱茏、生机勃勃,成为我市一道亮丽的风景.如图,从义乌江的南岸C点测得两处风景A、B两点的视角∠ECA和∠ACB分别为30°和105°,测得BC=100
商城义乌江的两岸绿树葱茏、生机勃勃,成为我市一道亮丽的风景.如图,从义乌江的南岸C点测得两处风景A、B两点的视角∠ECA和∠ACB分别为30°和105°,测得BC=100 已知,△ABC在平面直角坐标系中的位置如图所示,将△ABC以点O为中心逆时针旋转90°,则旋转后A点的坐标是
已知,△ABC在平面直角坐标系中的位置如图所示,将△ABC以点O为中心逆时针旋转90°,则旋转后A点的坐标是 在平面直角坐标系中,△ABC的位置如图所示,请解答下列问题:
在平面直角坐标系中,△ABC的位置如图所示,请解答下列问题: