题目内容
2.等式$\sqrt{{(x-1)}^{2}}$=1-x成立的条件是x≤1.分析 根据二次根式的性质得出1-x≥0,求出不等式的解集即可.
解答 解:∵$\sqrt{{(x-1)}^{2}}$=1-x,
∴1-x≥0,
∴x≤1,
故答案为:x≤1.
点评 本题考查了二次根式的性质和解一元一次不等式的应用,能得出关于x的不等式是解此题的关键,注意:当x≥0时,$\sqrt{{x}^{2}}$=x,当x≤0时,$\sqrt{{x}^{2}}$=-x.

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
10.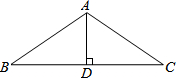 如图,已知AD⊥BC,D是垂足,BD=CD,下列判断:
如图,已知AD⊥BC,D是垂足,BD=CD,下列判断:
①△ABD≌△ACD;②△ABD与△ACD不全等;③AB=AC;④∠B=∠C;⑤AD平分∠BAC.
其中正确的是( )
 如图,已知AD⊥BC,D是垂足,BD=CD,下列判断:
如图,已知AD⊥BC,D是垂足,BD=CD,下列判断:①△ABD≌△ACD;②△ABD与△ACD不全等;③AB=AC;④∠B=∠C;⑤AD平分∠BAC.
其中正确的是( )
| A. | ①③④ | B. | ②③④⑤ | C. | ①③④⑤ | D. | ③⑤ |
9. 如图,已知点M为?ABCD的边AB的中点,线段CM交BD于点E,则图中阴影部分的面积与?ABCD面积的比是( )
如图,已知点M为?ABCD的边AB的中点,线段CM交BD于点E,则图中阴影部分的面积与?ABCD面积的比是( )
 如图,已知点M为?ABCD的边AB的中点,线段CM交BD于点E,则图中阴影部分的面积与?ABCD面积的比是( )
如图,已知点M为?ABCD的边AB的中点,线段CM交BD于点E,则图中阴影部分的面积与?ABCD面积的比是( )| A. | 1:2 | B. | 2:5 | C. | 3:5 | D. | 1:3 |
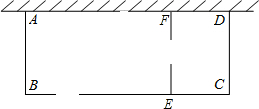 某养鸡专业户用篱笆及一面墙(该墙可用最大长度为36米)围成一个矩形场地ABCD来供鸡室外活动,该场地中间隔有一道与AB平行的篱笆(EF),如图,BE,EF上各留有1米宽的门(门不需要篱笆),该养鸡专业户共用篱笆58米,设该矩形的一边AB长x米,AD>AB,矩形ABCD的面积为S平方米.
某养鸡专业户用篱笆及一面墙(该墙可用最大长度为36米)围成一个矩形场地ABCD来供鸡室外活动,该场地中间隔有一道与AB平行的篱笆(EF),如图,BE,EF上各留有1米宽的门(门不需要篱笆),该养鸡专业户共用篱笆58米,设该矩形的一边AB长x米,AD>AB,矩形ABCD的面积为S平方米. 补全解答过程:
补全解答过程: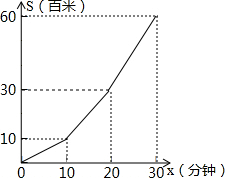 小明利用星期六、日双休骑自行车到城外小姨家去玩.星期六从家中出发,先上坡,后走平路,再走下坡路到小姨家.行程情况如图所示.星期日小明又沿原路返回自己家.若两天中,小明上坡、平路、下坡行驶的速度相对不变,则星期日,小明返回家的时间是43$\frac{1}{3}$分钟.
小明利用星期六、日双休骑自行车到城外小姨家去玩.星期六从家中出发,先上坡,后走平路,再走下坡路到小姨家.行程情况如图所示.星期日小明又沿原路返回自己家.若两天中,小明上坡、平路、下坡行驶的速度相对不变,则星期日,小明返回家的时间是43$\frac{1}{3}$分钟.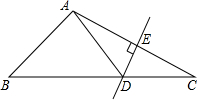 如图:△ABC中,DE是AC的垂直平分线,AE=3cm,△ABD的周长为13cm,则△ABC的周长为19.
如图:△ABC中,DE是AC的垂直平分线,AE=3cm,△ABD的周长为13cm,则△ABC的周长为19.