题目内容
13. 补全解答过程:
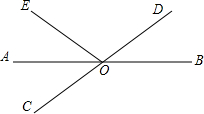
补全解答过程:已知:如图,直线AB、CD相交于点O,OA平分∠EOC,若∠EOC:∠EOD=2:3,求∠BOD的度数.
解:由题意∠EOC:∠EOD=2:3,
设∠EOC=2x°,则∠EOD=3x°.
∵∠EOC+∠EOD=180°(平角的定义),
∴2x+3x=180.
x=36.
∴∠EOC=72°.
∵OA平分∠EOC(已知),
∴∠AOC=$\frac{1}{2}$∠EOC=36°.
∵∠BOD=∠AOC(对顶角相等),
∴∠BOD=36°(等量代换)
分析 根据邻补角,可得方程,根据角平分线的定义,可得∠AOC的度数,根据对顶角相等,可得答案.
解答 解:由题意∠EOC:∠EOD=2:3,
设∠EOC=2x°,则∠EOD=3x°.
∵∠EOC+∠EOD=180°(平角的定义),
∴2x+3x=180.
x=36.
∴∠EOC=72°.
∵OA平分∠EOC(已知),
∴∠AOC=$\frac{1}{2}$∠EOC=36°.
∵∠BOD=∠AOC(对顶角相等),
∴∠BOD=36°(等量代换),
故答案为:EOD,平角的定义,对顶角相等,36°.
点评 本题考查了对顶角、邻补角,利用邻补角得出方程是解题关键,又利用了对顶角相等.

练习册系列答案
 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
4.表一、图1、图2是根据某初中学校2000名学生为四川雅安灾区捐款的情况而制作的统计图表.
(1)请你将表一、图1补充完整.
(2)该校九年级有660名学生.
(3)八年级的学生小明看了表一说:“我们八年级捐款最多,因此我们八年级学生最有爱心”.你认为小明的说法对吗?简单说说你的理由.
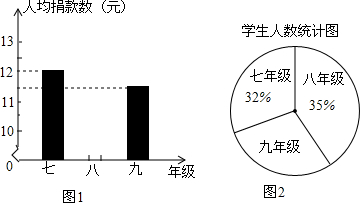
(1)请你将表一、图1补充完整.
| 年级 | 七年级 | 八年级 | 九年级 |
| 捐款(元) | 7680 | 7700 | 7590 |
(3)八年级的学生小明看了表一说:“我们八年级捐款最多,因此我们八年级学生最有爱心”.你认为小明的说法对吗?简单说说你的理由.

1.若$\left\{\begin{array}{l}x=3\\ y=2\end{array}\right.$是方程kx+3y=1的解,则k等于( )
| A. | $-\frac{5}{3}$ | B. | -4 | C. | $\frac{7}{3}$ | D. | $\frac{1}{4}$ |
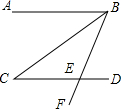 如图,已知AB∥CD,BC平分∠ABE,∠C=35°,则∠CEF的度数是70°.
如图,已知AB∥CD,BC平分∠ABE,∠C=35°,则∠CEF的度数是70°.