题目内容
12.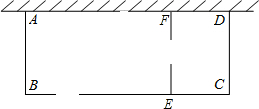 某养鸡专业户用篱笆及一面墙(该墙可用最大长度为36米)围成一个矩形场地ABCD来供鸡室外活动,该场地中间隔有一道与AB平行的篱笆(EF),如图,BE,EF上各留有1米宽的门(门不需要篱笆),该养鸡专业户共用篱笆58米,设该矩形的一边AB长x米,AD>AB,矩形ABCD的面积为S平方米.
某养鸡专业户用篱笆及一面墙(该墙可用最大长度为36米)围成一个矩形场地ABCD来供鸡室外活动,该场地中间隔有一道与AB平行的篱笆(EF),如图,BE,EF上各留有1米宽的门(门不需要篱笆),该养鸡专业户共用篱笆58米,设该矩形的一边AB长x米,AD>AB,矩形ABCD的面积为S平方米.(1)求出S与x的函数关系式,直接写出自变量x的取值范围;
(2)当x为何值时,S有最大值?求出这个最大值.[参考公式:二次函数y=ax2+bx+c(a≠0),当x=-$\frac{b}{2a}$时,y最大(小)值=$\frac{4ax-{b}^{2}}{4a}$.
分析 (1)根据题意可得BC-1=58-x-x-(x-1),求出BC的长即可列出S与x函数关系式;
(2)由(1)所得函数解析式,利用配方法即可求出函数最大值.
解答 解:(1)由题意得:BC-1=58-x-x-(x-1)=60-3x,
可得矩形ABCD的面积:S=x(60-3x)=-3x2+60x(8≤x<20);
(2)S=-3x2+60x=-3(x-10)2+300,
∵-3<0,
∴开口向下,S有最大值,
当x=10时,S取最大值300.
答:当x为10时,S有最大值300平方米.
点评 本题考查了二次函数的应用,解答本题的关键是结合题意利用长方形的面积列出函数关系式并掌握求二次函数最值的方法.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
2. 如图,顺次连结圆内接矩形各边的中点,得到菱形ABCD,若BD=8,BE=5,则菱形ABCD的边长为( )
如图,顺次连结圆内接矩形各边的中点,得到菱形ABCD,若BD=8,BE=5,则菱形ABCD的边长为( )
 如图,顺次连结圆内接矩形各边的中点,得到菱形ABCD,若BD=8,BE=5,则菱形ABCD的边长为( )
如图,顺次连结圆内接矩形各边的中点,得到菱形ABCD,若BD=8,BE=5,则菱形ABCD的边长为( )| A. | 6 | B. | $\sqrt{41}$ | C. | 9 | D. | $\sqrt{89}$ |
20.下列是正方体展开图的有( )


| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
4.表一、图1、图2是根据某初中学校2000名学生为四川雅安灾区捐款的情况而制作的统计图表.
(1)请你将表一、图1补充完整.
(2)该校九年级有660名学生.
(3)八年级的学生小明看了表一说:“我们八年级捐款最多,因此我们八年级学生最有爱心”.你认为小明的说法对吗?简单说说你的理由.
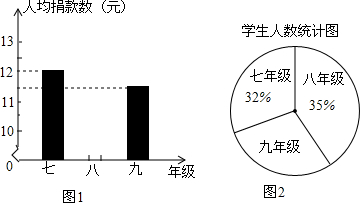
(1)请你将表一、图1补充完整.
| 年级 | 七年级 | 八年级 | 九年级 |
| 捐款(元) | 7680 | 7700 | 7590 |
(3)八年级的学生小明看了表一说:“我们八年级捐款最多,因此我们八年级学生最有爱心”.你认为小明的说法对吗?简单说说你的理由.

1.若$\left\{\begin{array}{l}x=3\\ y=2\end{array}\right.$是方程kx+3y=1的解,则k等于( )
| A. | $-\frac{5}{3}$ | B. | -4 | C. | $\frac{7}{3}$ | D. | $\frac{1}{4}$ |
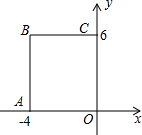 如图,在平面直角坐标系中,矩形OABC的顶点O在坐标原点,A(-4,0),C(0,6),如果矩形OA′B′C′与矩形OABC关于点O位似,且矩形OA′B′C′的面积等于矩形OABC面积的$\frac{1}{4}$,那么点B的对应点B′的坐标是(-2,3)或(2,-3).
如图,在平面直角坐标系中,矩形OABC的顶点O在坐标原点,A(-4,0),C(0,6),如果矩形OA′B′C′与矩形OABC关于点O位似,且矩形OA′B′C′的面积等于矩形OABC面积的$\frac{1}{4}$,那么点B的对应点B′的坐标是(-2,3)或(2,-3).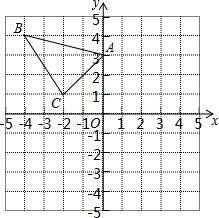 △ABC在直角坐标系内如所示.
△ABC在直角坐标系内如所示.