题目内容
9.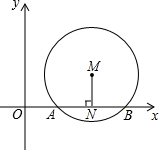 如图,在直角坐标系中,点M在第一象限内,MN⊥x轴于点N,MN=1,⊙M与x轴交于A(2,0)、B(6,0)两点.
如图,在直角坐标系中,点M在第一象限内,MN⊥x轴于点N,MN=1,⊙M与x轴交于A(2,0)、B(6,0)两点.(1)求⊙M的半径.
(2)在坐标轴上有一点P,过点P作垂直于坐标轴的直线l刚好和⊙M相切,请直接写出直线l的表达式.
分析 (1)可通过构建直角三角形来求解.连接AM,根据垂径定理我们不难得出AN=$\frac{1}{2}$AB,有了A,B的坐标,我们就知道了AB的长,也就有了AN的长.在直角三角形AMN中,知道了两条直角边AN,MN的长,就可以用勾股定理求出圆的半径了;
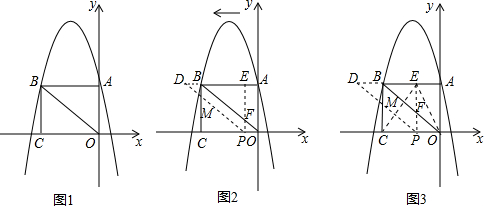
(2)根据题目的要求画出符合题意的图形,如图2所示,若过点P作垂直于坐标轴的直线l刚好和⊙M相切时,则求出OA,OP,OR,OK的值即可得到直线l的解析式.
解答 解:(1)连接MA,如图1
∵MN⊥AB于点N,
∴AN=BN,
∵A(2,0),B(6,0),
∴AB=4,
∴AN=2;
在Rt△AMN中,MN=1,AN=2,
∴AM=$\sqrt{{2}^{2}+{1}^{2}}$$\sqrt{5}$,
即⊙M的半径为$\sqrt{5}$;
(2) 如图所示:设直线l和圆分别相切于点C,H,F,E点,
如图所示:设直线l和圆分别相切于点C,H,F,E点,
∵A(2,0)、B(6,0),
∴AB=4,
∴AN=2,
∴ON=4,
∵CM=$\sqrt{5}$,
∴OG=ON-OG=4-$\sqrt{5}$,OP=4+$\sqrt{5}$,
∴直线l的解析法为x=4-$\sqrt{5}$或4+$\sqrt{5}$,
∵MN=1,
∴OR=NE=$\sqrt{5}$+1,OK=NH=$\sqrt{5}$-1,
∴直线l的解析法为y=$\sqrt{5}$+1或$\sqrt{5}$-1.
点评 本题主要考查了垂径定理,坐标与图形性质以及勾股定理等知识点的应用,通过构建直角三角形来求圆的半径是解题的基本思路.

练习册系列答案
相关题目
17.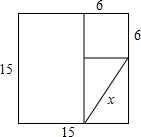 如图,在两个正方形和一个对角线长为x的矩形中,则x值应满足的范围是( )
如图,在两个正方形和一个对角线长为x的矩形中,则x值应满足的范围是( )
 如图,在两个正方形和一个对角线长为x的矩形中,则x值应满足的范围是( )
如图,在两个正方形和一个对角线长为x的矩形中,则x值应满足的范围是( )| A. | 8<x<9 | B. | 9<x<10 | C. | 10<x<11 | D. | 11<x<12 |
1.m为( )时,关于x的方程3x2+6x+m=0有两个负实数根.
| A. | 1,2 | B. | 1,2,3 | C. | 2,3 | D. | 1,3 |
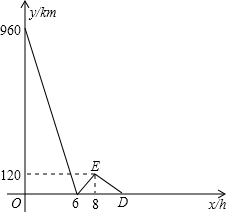 A、B两地之间的距离为960km,C地介于A、B两地之间,甲车从A地驶往C地,乙车从B地经C地驶往A地,已知两车同时出发,相向而行,结果两车同时到达C地后,甲车因故在C地须停留一段时间,然后返回A地,乙车继续驶往A地.设乙车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系.
A、B两地之间的距离为960km,C地介于A、B两地之间,甲车从A地驶往C地,乙车从B地经C地驶往A地,已知两车同时出发,相向而行,结果两车同时到达C地后,甲车因故在C地须停留一段时间,然后返回A地,乙车继续驶往A地.设乙车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系.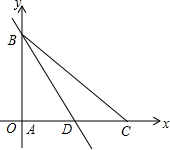 如图,△ABC中,∠BAC=90°,AB=AC=4,BD是AC边上的中线,分别以AC、AB所在直线为x轴、y轴建立直角坐标系.
如图,△ABC中,∠BAC=90°,AB=AC=4,BD是AC边上的中线,分别以AC、AB所在直线为x轴、y轴建立直角坐标系.