题目内容
17.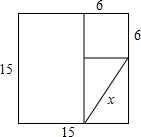 如图,在两个正方形和一个对角线长为x的矩形中,则x值应满足的范围是( )
如图,在两个正方形和一个对角线长为x的矩形中,则x值应满足的范围是( )| A. | 8<x<9 | B. | 9<x<10 | C. | 10<x<11 | D. | 11<x<12 |
分析 由正方形的性质和勾股定理得出x=3$\sqrt{13}$,即可得出x的取值范围.
解答 解:根据题意得:15-6=9,
由勾股定理得:x=$\sqrt{{6}^{2}+{9}^{2}}$=$\sqrt{117}$=3$\sqrt{13}$,
∵10<3$\sqrt{13}$<11,
∴x的取值范围是10<x<11;
故选:C.
点评 本题考查了正方形的性质、勾股定理;熟练掌握正方形的性质,运用勾股定理求出x是解决问题的关键.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
8.已知点M(-2,3)在双曲线y=$\frac{k}{x}$上,则下列各点一定在该双曲线上的是( )
| A. | (3,-2) | B. | (-2,-3) | C. | (2,3) | D. | (3,2) |
5.下列各曲线中,哪些表示y是x的函数( )


| A. | ①②③ | B. | ②③④ | C. | ①③④ | D. | ①②④ |
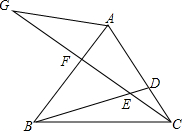 在等边△ABC中,D、F两点分别在边AC、AB上,AF=CD,连接BD、CF,并延长CF至点G,连接AG,且∠G=30°.若BE=10,CE=6,则CG=22.
在等边△ABC中,D、F两点分别在边AC、AB上,AF=CD,连接BD、CF,并延长CF至点G,连接AG,且∠G=30°.若BE=10,CE=6,则CG=22.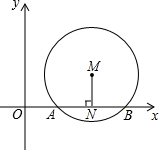 如图,在直角坐标系中,点M在第一象限内,MN⊥x轴于点N,MN=1,⊙M与x轴交于A(2,0)、B(6,0)两点.
如图,在直角坐标系中,点M在第一象限内,MN⊥x轴于点N,MN=1,⊙M与x轴交于A(2,0)、B(6,0)两点.