题目内容
6.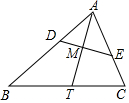 如图,点M是△ABC的角平分线AT的中点,点D、E分别在AB、AC边上,线段DE过点M,且∠ADE=∠C,那么△ADE和△ABC的面积比是1:4.
如图,点M是△ABC的角平分线AT的中点,点D、E分别在AB、AC边上,线段DE过点M,且∠ADE=∠C,那么△ADE和△ABC的面积比是1:4.
分析 根据相似三角形的判定和性质即可得到结论.
解答 解:∵AT是△ABC的角平分线,
∵点M是△ABC的角平分线AT的中点,
∴AM=$\frac{1}{2}$AT,
∵∠ADE=∠C,∠BAC=∠BAC,
∴△ADE∽△ACB,
∴$\frac{{S}_{△ADE}}{{S}_{△ACB}}$=($\frac{AM}{AT}$)2=($\frac{1}{2}$)2=1:4,
故答案为:1:4.
点评 本题考查了相似三角形的判定和性质,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
14.若代数式xy2与-3xm-1y2n的和是-2xy2,则2m+n的值是( )
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
1. 如图所示的几何体从上面看得到的平面图形是( )
如图所示的几何体从上面看得到的平面图形是( )
 如图所示的几何体从上面看得到的平面图形是( )
如图所示的几何体从上面看得到的平面图形是( )| A. |  | B. |  | C. |  | D. |  |
18.在0,|-5|,-(-2),-32各数中,负数的个数是( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
16.计算:a•a2的结果是( )
| A. | 3a | B. | a3 | C. | 2a2 | D. | 2a3 |
 如图,△ABC中,点D在边AB上,满足∠ACD=∠ABC,若AC=$\sqrt{3}$,AD=1,求DB的长.
如图,△ABC中,点D在边AB上,满足∠ACD=∠ABC,若AC=$\sqrt{3}$,AD=1,求DB的长.