题目内容
17.已知(x+$\frac{\sqrt{2}}{2}$)2+$\sqrt{y-\sqrt{2}}$=0,试求(xy)2010的值.分析 直接利用偶次方的性质结合二次根式的性质得出x,y的值,即可得出答案.
解答 解:∵(x+$\frac{\sqrt{2}}{2}$)2+$\sqrt{y-\sqrt{2}}$=0,
∴x=-$\frac{\sqrt{2}}{2}$,y=$\sqrt{2}$,
∴(xy)2010=(-$\frac{\sqrt{2}}{2}$×$\sqrt{2}$)2010
=1.
点评 此题主要考查了偶次方的性质和二次根式的性质,正确得出x,y的值是解题关键.

练习册系列答案
相关题目
7.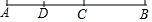 如图,C、D是线段AB上两点,若BC=3cm,BD=5cm,且D是AC的中点,则AC的长为( )
如图,C、D是线段AB上两点,若BC=3cm,BD=5cm,且D是AC的中点,则AC的长为( )
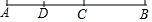 如图,C、D是线段AB上两点,若BC=3cm,BD=5cm,且D是AC的中点,则AC的长为( )
如图,C、D是线段AB上两点,若BC=3cm,BD=5cm,且D是AC的中点,则AC的长为( )| A. | 2cm | B. | 4cm | C. | 8cm | D. | 13cm |
8.法国的“小九九”从“一一得一”到“五五二十五”和我国的“小九九”是一样的,后面的就改用手势了.下面两个图框是用法国“小九九”计算7×8和8×9的两个示例,且左手伸出的手指数不大于右手伸出的手指数.若用法国的“小九九”计算7×9,左、右手依次伸出手指的个数是( )


| A. | 2,4 | B. | 1,4 | C. | 3,4 | D. | 3,1 |
5.在平面直角坐标系中,将抛物线y=x2+2x+3绕着原点旋转180°,所得抛物线的解析式是( )
| A. | y=(x+1)2-2 | B. | y=-(x-1)2-2 | C. | y=-(x-1)2+2 | D. | y=(x-1)2-2 |
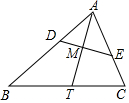 如图,点M是△ABC的角平分线AT的中点,点D、E分别在AB、AC边上,线段DE过点M,且∠ADE=∠C,那么△ADE和△ABC的面积比是1:4.
如图,点M是△ABC的角平分线AT的中点,点D、E分别在AB、AC边上,线段DE过点M,且∠ADE=∠C,那么△ADE和△ABC的面积比是1:4.