题目内容

16．解不等式组：$\left\{\begin{array}{l}{x-3（x-2）≥4}\\{\frac{2x-1}{5}＜\frac{x+1}{2}}\end{array}\right.$．

分析 首先解出不等式组中的x的取值范围，然后找出它们的公共部分，该公共部分就是不等式组的解集．

解答 解：不等式（1）可化为x-3x+6≥4，
解得x≤1，
不等式（2）可化为2（2x-1）＜5（x+1），
4x-2＜5x+5，
解得x＞-7．
把解集表示在数轴上为：

∴原不等式组的解集为-7＜x≤1．

点评 本题考查解不等式组，求出不等式公共解集，要遵循以下原则：同大取较大，同小取较小，小大大小中间找，大大小小解不了．

练习册系列答案
相关题目
6．分解因式：x2（y-z）+y2（z-x）+z2（x-y）=（x-z）（ x-y）（y-z）．
7．如图，∠BAC=40°，直线l⊥AC，l与AB交于点D，将∠BAC沿直线l翻折，点A落在AC边上点F处，则∠BDF的大小为80度．
4．如图，从A到B的四条路径中，最短的路线是（　　）
A．A-E-G-BB．A-E-C-BC．A-E-G-D-BD．A-E-F-B
11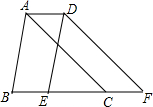．如图，将△ABC沿BC方向平移2cm得到△DEF，若△ABC的周长为18cm，则四边形ABFD的周长为（　　）
A．16cmB．18cmC．22cmD．20cm
1．若整式x2+9y2-pxy是完全平方式，则实数p的值为（　　）
A．-6B．-9C．±6D．±9
8．已知△ABC的面积是60，请完成下列问题：
（1）如图1，若AD是△ABC的BC边上的中线，则△ABD的面积=△ACD的面积（填“＞”“＜”或“=”）
（2）如图2，若CD、BE分别是△ABC的AB、AC边上的中线，求四边形ADOE的面积可以用如下方法：连接AO，由AD=DB得：S△ADO=S△BDO，同理：S△CEO=S△AEO，设S△ADO=x，S△CEO=y，则S△BDO=x，S△AEO=y由题意得：S△ABE=$\frac{1}{2}$S△ABC=30，S△ADC=$\frac{1}{2}$S△ABC=30，可列方程组为：$\left\{\begin{array}{l}{2x+y=30}\\{x+2y=30'}\end{array}\right.$，解得$\left\{\begin{array}{l}{x=10}\\{y=10}\end{array}\right.$，通过解这个方程组可得四边形ADOE的面积为20．
（3）如图3，AD：DB=1：3，CE：AE=1：2，请你计算四边形ADOE的面积，并说明理由．
5．将一个小球在如图所示的地砖上自由滚动，最终没有停在黑色方砖上的概率为（　　）
A．$\frac{1}{3}$B．$\frac{4}{9}$C．$\frac{1}{2}$D．$\frac{5}{9}$
6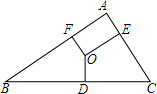．如图，O是△ABC的外心，OD⊥BC，OE⊥AC，OF⊥AB，则OD：OE：OF等于（　　）
A．a：b：cB．$\frac{1}{a}$：$\frac{1}{b}$：$\frac{1}{c}$C．sinA：sinB：sinCD．cosA：cosB：cosC

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网