题目内容
7．
如图，∠BAC=40°，直线l⊥AC，l与AB交于点D，将∠BAC沿直线l翻折，点A落在AC边上点F处，则∠BDF的大小为80度．
分析 由折叠的性质可知∠DFA=∠A=40°，再根据三角形外角和定理即可求出∠BDF的大小．
解答 解：∵将∠BAC沿直线l翻折，点A落在AC边上点F处，
∴∠DFA=∠A=40°，
∴∠BDF=∠A+∠DFA=80°，
故答案为：80．
点评 本题考查了折叠的性质以及三角形外角和定理的运用，解题的关键是熟练掌握折叠的性质：折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．
练习册系列答案
相关题目
17．如果x1，x2是一元二次方程x2+8x+3=0的两个实数根，那么x1+x2的值是（ ）
| A． | -8 | B． | 8 | C． | 3 | D． | -3 |
2．
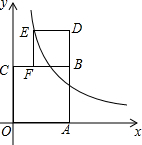如图，四边形OABC、BDEF是面积分别为S1、S2的正方形，点A在x轴上，点F在BC上，点E在反比例函数y=$\frac{k}{x}$（k＞0）的图象上，若S1-S2=2，则k值为（ ）
如图，四边形OABC、BDEF是面积分别为S1、S2的正方形，点A在x轴上，点F在BC上，点E在反比例函数y=$\frac{k}{x}$（k＞0）的图象上，若S1-S2=2，则k值为（ ）| A． | 1 | B． | $\sqrt{2}$ | C． | 2 | D． | 4 |
12．
如图所示，点C在以AB为直径的⊙O上，∠A=20°，则∠BOC等于（ ）
如图所示，点C在以AB为直径的⊙O上，∠A=20°，则∠BOC等于（ ）| A． | 20° | B． | 30° | C． | 40° | D． | 50° |