题目内容
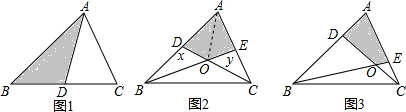
8.已知△ABC的面积是60,请完成下列问题:(1)如图1,若AD是△ABC的BC边上的中线,则△ABD的面积=△ACD的面积(填“>”“<”或“=”)
(2)如图2,若CD、BE分别是△ABC的AB、AC边上的中线,求四边形ADOE的面积可以用如下方法:连接AO,由AD=DB得:S△ADO=S△BDO,同理:S△CEO=S△AEO,设S△ADO=x,S△CEO=y,则S△BDO=x,S△AEO=y由题意得:S△ABE=$\frac{1}{2}$S△ABC=30,S△ADC=$\frac{1}{2}$S△ABC=30,可列方程组为:$\left\{\begin{array}{l}{2x+y=30}\\{x+2y=30'}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=10}\\{y=10}\end{array}\right.$,通过解这个方程组可得四边形ADOE的面积为20.
(3)如图3,AD:DB=1:3,CE:AE=1:2,请你计算四边形ADOE的面积,并说明理由.
分析 (1)根据等底等高的两个三角形面积相等知,三角形的中线把三角形的面积分为相等的两部分,所以S△ABD=S△ACD;
(2)根据三角形的中线能把三角形的面积平分,等高三角形的面积的比等于底的比,即可得到结果;
(3)连结AO,由AD:DB=1:3,得到S△ADO=$\frac{1}{3}$S△BDO,同理可得S△CEO=$\frac{1}{2}$S△AEO,设S△ADO=x,S△CEO=y,则S△BDO=3x,S△AEO=2y,由题意得列方程组即可得到结果.
解答 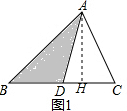 解:(1)如图1,过A作AH⊥BC于H,
解:(1)如图1,过A作AH⊥BC于H,
∵AD是△ABC的BC边上的中线,
∴BD=CD,
∴${S}_{△ABD}=\frac{1}{2}BD•AH$,${S}_{△ACD}=\frac{1}{2}CD•AH$,
∴S△ABD=S△ACD,
故答案为:=;
(2)解方程组得$\left\{\begin{array}{l}{x=10}\\{y=10}\end{array}\right.$,
∴S△AOD=S△BOD=10,
∴S四边形ADOB=S△AOD+S△AOE=10+10=20,
故答案为:得$\left\{\begin{array}{l}{x=10}\\{y=10}\end{array}\right.$,20;
(3)如图3,连结AO,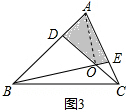
∵AD:DB=1:3,
∴S△ADO=$\frac{1}{3}$S△BDO,
∵CE:AE=1:2,
∴S△CEO=$\frac{1}{2}$S△AEO,
设S△ADO=x,S△CEO=y,则S△BDO=3x,S△AEO=2y,
由题意得:S△ABE=$\frac{2}{3}$S△ABC=40,S△ADC=$\frac{1}{4}$S△ABC=15,
可列方程组为:$\left\{\begin{array}{l}{x+3y=15}\\{4x+2y=40}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=9}\\{y=2}\end{array}\right.$,
∴S四边形ADOE=S△ADO+S△AEO=x+2 y=13.
点评 本题考查了三角形的中线能把三角形的面积平分,等高三角形的面积的比等于底的比,熟练掌握这个结论是解题的关键.

 阳阳离开家去新华书店买书,回来后,阳阳用所学知识绘制了一张反映他离家的距离与时间的关系图,请根据阳阳绘制的这张图回答以下问题:
阳阳离开家去新华书店买书,回来后,阳阳用所学知识绘制了一张反映他离家的距离与时间的关系图,请根据阳阳绘制的这张图回答以下问题: