题目内容
6.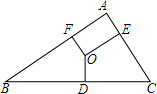 如图,O是△ABC的外心,OD⊥BC,OE⊥AC,OF⊥AB,则OD:OE:OF等于( )
如图,O是△ABC的外心,OD⊥BC,OE⊥AC,OF⊥AB,则OD:OE:OF等于( )| A. | a:b:c | B. | $\frac{1}{a}$:$\frac{1}{b}$:$\frac{1}{c}$ | C. | sinA:sinB:sinC | D. | cosA:cosB:cosC |
分析 作出△ABC的外接圆,连接OA、OB、OC,由垂径定理和圆周角定理可得∠B=$\frac{1}{2}$∠AOC=∠AOE,同理可知∠A=∠BOD、∠C=∠AOF,若设⊙O的半径为R,可用R分别表示出OD、OE、OF,进而可得到它们的比例关系.
解答  解:如图,连接OA、OB、OC;
解:如图,连接OA、OB、OC;
∵∠BOC=2∠BAC=2∠BOD,
∴∠BAC=∠BOD;
同理可得:∠BOF=∠BCA,∠AOE=∠ABC;
设⊙O的半径为R,则:
OD=R•cos∠BOD=R•cos∠A,
OE=R•cos∠AOE=R•cos∠B,
OF=R•cos∠BOF=R•cos∠C,
故OD:OE:OF=cos∠A:cos∠B:cos∠C,
故选D.
点评 此题主要考查了三角形的外接圆、圆周角定理及垂径定理的综合应用,解题的关键是能够作出已知三角形的外接圆,难度中等.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案
相关题目
14.下列计算正确的是( )
| A. | x2•x4=x8 | B. | (-a)2•a5=a7 | C. | 5×59=50 | D. | (-a)a5=-a5 |
16.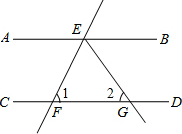 如图,已知AB∥CD,直线EF分别交 AB、CD于点E,F,EG平分∠BEF交CD于点G.如果∠1=70°,那么∠2的度数是( )
如图,已知AB∥CD,直线EF分别交 AB、CD于点E,F,EG平分∠BEF交CD于点G.如果∠1=70°,那么∠2的度数是( )
 如图,已知AB∥CD,直线EF分别交 AB、CD于点E,F,EG平分∠BEF交CD于点G.如果∠1=70°,那么∠2的度数是( )
如图,已知AB∥CD,直线EF分别交 AB、CD于点E,F,EG平分∠BEF交CD于点G.如果∠1=70°,那么∠2的度数是( )| A. | 70° | B. | 65° | C. | 55° | D. | 22.5° |