题目内容
12．
如图，在Rt△ABC中，∠ACB=90°，CD⊥AB，AC=7，BC=24，求tan∠ACD的值．
分析 根据已知条件和余角的性质得到∠ACD=∠B=90°-∠A，然后根据三角函数的定义即可得到结论．
解答 解：∵∠ACB=90°，CD⊥AB于D，
∴∠ACD=∠B=90°-∠A，
∴tan∠ACD=tan∠B=$\frac{AC}{BC}$=$\frac{7}{24}$．
点评 本题考查了解直角三角形，锐角三角函数的定义，熟记锐角三角函数的定义是解题的关键．
练习册系列答案
期末好成绩系列答案
99加1领先期末特训卷系列答案
百强名校期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案
金状元绩优好卷系列答案
相关题目
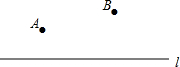如图，已知直线l及其同侧两点A、B．
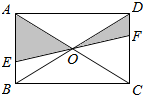如图所示，EF过矩形ABCD对角线的交点O，且分别交AB，CD于点E，F，若AB=3，BC=4，那么阴影部分的面积为（ ）
20．抛物线y=-x2-4x经过坐标原点，与x轴交于点A，该抛物线上存在点P，满足S△AOP=8，则点P的坐标是（-2，4）或（-2$\sqrt{2}$-2，0）或，2$\sqrt{2}$-2，0）．
如图，已知不等边三角形ABC．求作：作一个三角形，使它与△ABC有公共顶点C，并且与△ABC全等（不写作法，保留作图痕迹）．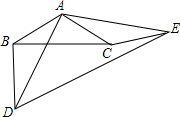
如图所示，△ABC，△ADE均是顶角为120°的等腰三角形，BC，DE分别是它们的底边，图中的哪两个三角形可以通过怎样的旋转而相互得到？
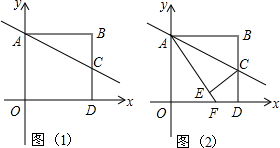如图（1），四边形AODB是边长为2的正方形，C为BD的中点，以O为原点，OA、OD所在直线为坐标轴建立平面直角坐标系．
1．在2-[2（x+y）-（ ）]=x+2中，括号内填的式子应是（ ）
| A． | 3x+2y | B． | -x+2y | C． | x-2y | D． | -x-2y |