题目内容
17. 如图,EG、FG分别是∠MEF,∠NFE的平分线,交点是G,BP,CP分别是∠MBC和∠NCB的平分线,交点是P.
如图,EG、FG分别是∠MEF,∠NFE的平分线,交点是G,BP,CP分别是∠MBC和∠NCB的平分线,交点是P.(1)证明:A,P,G三点共线;
(2)若∠G=68°,求∠P的度数.
分析 (1)根据角平分线的性质即可得到结论;
(2)根据角平分线的定义和三角形内角和定理用∠A表示∠Q和∠P,得到∠Q和∠P的关系,得到答案.
解答 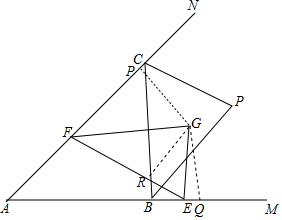 解:(1)过G作GP⊥AN于P,GQ⊥AM于Q,PR⊥EF于R,
解:(1)过G作GP⊥AN于P,GQ⊥AM于Q,PR⊥EF于R,
∵EG、FG分别是∠MEF,∠NFE的平分线,
∴GP=GR=GQ,
∴G在∠NAN的角平分线上,
同理点P在∠NAN的角平分线上,
∴A,P,G三点共线;
(2)∵EQ、FQ分别是∠MEF和∠NFE的平分线,
∴∠QFE=$\frac{1}{2}$∠NFE,∠QEF=$\frac{1}{2}$∠MEF,
∴∠Q=180°-$\frac{1}{2}$∠NFE-$\frac{1}{2}$∠MEF
=180°-$\frac{1}{2}$(∠NFE+∠MEF)
=180°-$\frac{1}{2}$(360°-∠AFE-∠AEF)
=180°-$\frac{1}{2}$(180°+∠A)
=90°-$\frac{1}{2}$∠A=68°,
同理,∠P=90°-$\frac{1}{2}$∠A=68°.
点评 本题考查的是角平分线的性质,角平分线的定义和三角形内角和定理,掌握三角形内角和等于180°是解题的关键.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案 优加精卷系列答案
优加精卷系列答案
相关题目
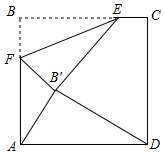 如图,正方形ABCD的边长为8,E为BC上一定点,BE=6,F为AB上一动点,把△BEF沿EF折叠,点B落在点B'处,当△AFB'恰好为直角三角形,B'D的长为$\frac{4}{5}\sqrt{65}$或2$\sqrt{2}$.
如图,正方形ABCD的边长为8,E为BC上一定点,BE=6,F为AB上一动点,把△BEF沿EF折叠,点B落在点B'处,当△AFB'恰好为直角三角形,B'D的长为$\frac{4}{5}\sqrt{65}$或2$\sqrt{2}$. 如图,己知AB=8,以AB为斜边作Rt△ABC,∠ACB=90°,过点C作AB的平行线,再过点A作AB的垂线,使两线相交于点D.设AC=x,DC=y,则(x-y)的最大值是( )
如图,己知AB=8,以AB为斜边作Rt△ABC,∠ACB=90°,过点C作AB的平行线,再过点A作AB的垂线,使两线相交于点D.设AC=x,DC=y,则(x-y)的最大值是( )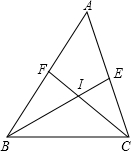 如图,在△ABC中,BE,CF是角平分线,它们相交于点I,求证:∠BIC=90°+$\frac{1}{2}$∠BAC.
如图,在△ABC中,BE,CF是角平分线,它们相交于点I,求证:∠BIC=90°+$\frac{1}{2}$∠BAC.