题目内容
9.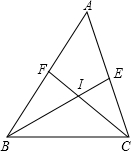 如图,在△ABC中,BE,CF是角平分线,它们相交于点I,求证:∠BIC=90°+$\frac{1}{2}$∠BAC.
如图,在△ABC中,BE,CF是角平分线,它们相交于点I,求证:∠BIC=90°+$\frac{1}{2}$∠BAC.
分析 根据角平分线的定义可得∠IBC=$\frac{1}{2}$∠ABC,∠ICB=$\frac{1}{2}$∠ACB,然后表示出∠IBC+∠ICB,再根据三角形的内角和等于180°列式整理即可得证.
解答 证明:∵∠ABC与∠ACB的平分线相交于点I,
∴∠IBC=$\frac{1}{2}$∠ABC,∠ICB=$\frac{1}{2}$∠ACB,
∴∠IBC+∠ICB=$\frac{1}{2}$(∠ABC+∠ACB),
在△IBC中,∠BIC=180°-(∠IBC+∠ICB)
=180°-$\frac{1}{2}$(∠ABC+∠ACB)
=180°-$\frac{1}{2}$(180°-∠BAC)
=90°+$\frac{1}{2}$∠BAC,
即:∠BIC=90°+$\frac{1}{2}$∠BAC.
点评 本题考查了三角形的内角和定理,角平分线的定义,整体思想的利用是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.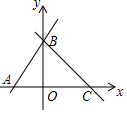 如图,在平面直角坐标系xOy中,直线AB交x轴于点A、交y轴于点B,且∠BAO=60°,直线BC垂直AB于点B,交x轴于点C,若A(-2,0),则点C的坐标为( )
如图,在平面直角坐标系xOy中,直线AB交x轴于点A、交y轴于点B,且∠BAO=60°,直线BC垂直AB于点B,交x轴于点C,若A(-2,0),则点C的坐标为( )
 如图,在平面直角坐标系xOy中,直线AB交x轴于点A、交y轴于点B,且∠BAO=60°,直线BC垂直AB于点B,交x轴于点C,若A(-2,0),则点C的坐标为( )
如图,在平面直角坐标系xOy中,直线AB交x轴于点A、交y轴于点B,且∠BAO=60°,直线BC垂直AB于点B,交x轴于点C,若A(-2,0),则点C的坐标为( )| A. | (3$\sqrt{2}$,0) | B. | (6,0) | C. | (3$\sqrt{3}$,0) | D. | (5,0) |
19. 如图,图中可以只用一个大写字母表示的角有( )
如图,图中可以只用一个大写字母表示的角有( )
 如图,图中可以只用一个大写字母表示的角有( )
如图,图中可以只用一个大写字母表示的角有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
 如图,长方体中所有与棱AB平行的棱是DC,EF,HM.
如图,长方体中所有与棱AB平行的棱是DC,EF,HM. 如图,EG、FG分别是∠MEF,∠NFE的平分线,交点是G,BP,CP分别是∠MBC和∠NCB的平分线,交点是P.
如图,EG、FG分别是∠MEF,∠NFE的平分线,交点是G,BP,CP分别是∠MBC和∠NCB的平分线,交点是P. 如图,已知AB∥CD,BP和CP分别平分∠ABC和∠DCB,AD过点P,且与AB垂直.若AP=4,则AD=( )
如图,已知AB∥CD,BP和CP分别平分∠ABC和∠DCB,AD过点P,且与AB垂直.若AP=4,则AD=( )