题目内容
2.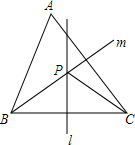 如图,锐角三角形ABC中,直线L为BC的中垂线,直线M为∠ABC的角平分线,L与M相交于P点.若∠A=60°,∠ACP=21°,则∠ABP的度数为33°.
如图,锐角三角形ABC中,直线L为BC的中垂线,直线M为∠ABC的角平分线,L与M相交于P点.若∠A=60°,∠ACP=21°,则∠ABP的度数为33°.
分析 根据角平分线定义求出∠ABP=∠CBP,根据线段的垂直平分线性质得出BP=CP,求出∠CBP=∠BCP,根据三角形内角和定理得出方程3∠ABP+21°+60°=180°,求出方程的解即可.
解答 解:∵BP平分∠ABC,
∴∠ABP=∠CBP,
∵直线l是线段BC的垂直平分线,
∴BP=CP,
∴∠CBP=∠BCP,
∴∠ABP=∠CBP=∠BCP,
∵∠A+∠ACB+∠ABC=180°,∠A=60°,∠ACP=21°,
∴3∠ABP+21°+60°=180°,
解得:∠ABP=33°.
故答案为:33°.
点评 本题考查了三角形内角和定理,线段垂直平分线性质,等腰三角形的性质的应用,能求出∠ABP=∠CBP=∠BCP是解此题的关键,数形结合思想的应用.

练习册系列答案
相关题目
14.下列说法错误的是( )
| A. | 全等三角形的三条边相等,三个角也相等 | |
| B. | 判定两个三角形全等的条件中至少有一个是边 | |
| C. | 面积相等的两个图形是全等形 | |
| D. | 全等三角形的面积和周长都相等 |
11.将抛物线向左平移2个单位,再向下平移3个单位后,所得抛物线的解析式为y=x2-1,则原抛物线的解析式为( )
| A. | y=x2+3 | B. | y=x2-3 | C. | y=(x+2)2-3 | D. | y=(x-2)2+2 |