题目内容
3.2010年5月1日,第41届世博会在上海举办,世博知识在校园迅速传播.小明同学就本班学生对世博知识的了解程度进行了一次调查统计,下图是他采集数据后绘制的两幅不完整的统计图(A:不了解,B:一般了解,C:了解较多,D:熟悉).请你根据图中提供的信息解答以下问题:(1)求该班共有50名学生,“了解较多”部分所对应的圆心角的度数为144°;
(2)从该班中任选一人,其对世博知识的了解程度为“熟悉”的概率是多少?
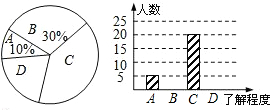
分析 (1)根据A是5人,占总体的10%,即可求得总人数;再用360°乘以“了解较多”所占的百分比,即可求出“了解较多”部分所对应的圆心角的度数;
(2)先求出一般了解的人数,再求出熟悉的人数,然后根据概率公式即可得出答案.
解答 解:(1)根据题意得:5÷10%=50(人).
“了解较多”部分所对应的圆心角的度数为360×$\frac{20}{50}$=144°;
故答案为:50,144°;
(2)一般了解的人数有50×30%=15(人),
则了解程度为“熟悉”的概率是:$\frac{50-5-15-20}{50}$=$\frac{1}{5}$.
点评 此题考查了条形统计图、扇形统计图和概率公式,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.总体数目=部分数目÷相应百分比.部分数目=总体数目乘以相应概率.概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
18.如图,在长方形形ABCD中,动点P从点B出发,沿BC、CD、DA运动至A停止,设点P运动的路程为x,△ABP的面积为y,如果y关于x的函数图象如图2所示,则△ABC的面积是( )


| A. | 16 | B. | 10 | C. | 18 | D. | 20 |
12.下列说法正确的是( )
| A. | 2πx2的系数是2 | B. | -xy2的次数为2 | C. | -5x2+x=-4x3 | D. | 3x2-x2=2x2 |
13. 如图,已知∠ABC=∠DCB,下列所给条件不能证明△ABC≌△DCB的是( )
如图,已知∠ABC=∠DCB,下列所给条件不能证明△ABC≌△DCB的是( )
 如图,已知∠ABC=∠DCB,下列所给条件不能证明△ABC≌△DCB的是( )
如图,已知∠ABC=∠DCB,下列所给条件不能证明△ABC≌△DCB的是( )| A. | ∠A=∠D | B. | AC=BD | C. | ∠ACB=∠DBC | D. | AB=DC |
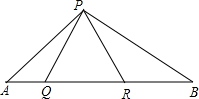 如图,△PQR为等边三角形,∠APB=120°,若AQ=4,QR=6,则BR=9.
如图,△PQR为等边三角形,∠APB=120°,若AQ=4,QR=6,则BR=9. 如图,点B、F、C、E在一条直线上,∠B=∠E,AC∥FD,BF=CE.求证:AB=DE.
如图,点B、F、C、E在一条直线上,∠B=∠E,AC∥FD,BF=CE.求证:AB=DE.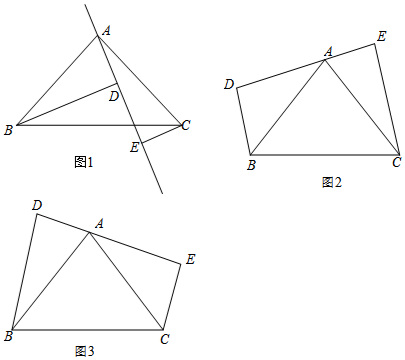
 如图,⊙O的半径为1,点A、P、B、C是⊙O上的四个点,∠APC=∠CPB=60°.
如图,⊙O的半径为1,点A、P、B、C是⊙O上的四个点,∠APC=∠CPB=60°.