题目内容
9.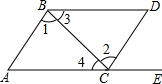 如图,点E在AC的延长线上,对于给出的四个条件:
如图,点E在AC的延长线上,对于给出的四个条件:①∠3=∠4;②∠1=∠2;③∠A=∠DCE;④∠D+∠ABD=180°.
能判断AB∥CD的是( )
| A. | ②③ | B. | ②③④ | C. | ②③ | D. | ①②③④ |
分析 根据平行线的判定定理即可直接作出判断.
解答 解:①根据内错角相等,两直线平行即可证得BD∥AC,不能证明AB∥CD;
②根据内错角相等,两直线平行即可证得AB∥CD;
③根据同位角相等,两直线平行即可证得AB∥CD;
④根据同旁内角互补,两直线平行,即可证得AB∥CD.
故选B
点评 本题考查了平行线的判定定理,正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键,不能遇到相等或互补关系的角就误认为具有平行关系,只有同位角相等、内错角相等、同旁内角互补,才能推出两被截直线平行.

练习册系列答案
相关题目
19.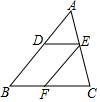 已知在△ABC中,点D为AB上一点,过点D作BC的平行线交AC于点E,过点E作AB的平行线交BC于点F.则下列说法不正确的是( )
已知在△ABC中,点D为AB上一点,过点D作BC的平行线交AC于点E,过点E作AB的平行线交BC于点F.则下列说法不正确的是( )
 已知在△ABC中,点D为AB上一点,过点D作BC的平行线交AC于点E,过点E作AB的平行线交BC于点F.则下列说法不正确的是( )
已知在△ABC中,点D为AB上一点,过点D作BC的平行线交AC于点E,过点E作AB的平行线交BC于点F.则下列说法不正确的是( )| A. | $\frac{AD}{AB}$=$\frac{AE}{AC}$ | B. | $\frac{DE}{BC}$=$\frac{AE}{AC}$ | C. | $\frac{AD}{AB}$=$\frac{BF}{FC}$ | D. | $\frac{DE}{BC}$=$\frac{AD}{AB}$ |
17.以下各数$\frac{22}{7}$,3.14159265,$\sqrt{7}$,-8,$\root{3}{2}$,0.6060060006…,0,$\sqrt{36}$,$\frac{π}{3}$,无理数的个数有( )
| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
1.△ABC∽△DEF,且它们的周长之比为2:3,则它们的面积之比为( )
| A. | 2:3 | B. | 4:6 | C. | 4:9 | D. | 3:2 |
18.既是方程2x-y=3的解,又是方程3x-4y=2的解的是( )
| A. | $\left\{\begin{array}{l}x=1\\ y=2\end{array}\right.$ | B. | $\left\{\begin{array}{l}x=2\\ y=1\end{array}\right.$ | C. | $\left\{\begin{array}{l}x=4\\ y=3\end{array}\right.$ | D. | $\left\{\begin{array}{l}x=-4\\ y=-5\end{array}\right.$ |
19.若x、y为实数,且$\sqrt{2x-1}$$+\sqrt{1-2x}$+y=4,则xy的值是( )
| A. | 0 | B. | $\frac{1}{2}$ | C. | 2 | D. | 4 |
 如图,按角的位置关系填空:∠3与∠2是内错角;∠B 与∠3 是同旁内角.
如图,按角的位置关系填空:∠3与∠2是内错角;∠B 与∠3 是同旁内角.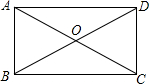 如图,在矩形ABCD中,AB=5cm,且∠BOC=120°,则AC的长为10cm.
如图,在矩形ABCD中,AB=5cm,且∠BOC=120°,则AC的长为10cm.