题目内容
19.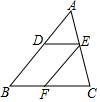 已知在△ABC中,点D为AB上一点,过点D作BC的平行线交AC于点E,过点E作AB的平行线交BC于点F.则下列说法不正确的是( )
已知在△ABC中,点D为AB上一点,过点D作BC的平行线交AC于点E,过点E作AB的平行线交BC于点F.则下列说法不正确的是( )| A. | $\frac{AD}{AB}$=$\frac{AE}{AC}$ | B. | $\frac{DE}{BC}$=$\frac{AE}{AC}$ | C. | $\frac{AD}{AB}$=$\frac{BF}{FC}$ | D. | $\frac{DE}{BC}$=$\frac{AD}{AB}$ |
分析 由平行线分线段成比例定理即可得出结论.
解答 解:∵DE∥BC,EF∥AB,
∴$\frac{AD}{AB}=\frac{AE}{AC}$=$\frac{DE}{BC}$,A、B、D选项正确;
∵四边形BDEF是平行四边形,
∴DE=BF,
∴$\frac{AD}{AB}=\frac{DE}{BC}=\frac{BF}{BC}$,故C选项错误;
故选:C.
点评 本题考查了平行线分线段成比例定理;熟练掌握平行线分线段成比例定理是解决问题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
9.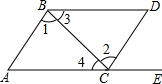 如图,点E在AC的延长线上,对于给出的四个条件:
如图,点E在AC的延长线上,对于给出的四个条件:
①∠3=∠4;②∠1=∠2;③∠A=∠DCE;④∠D+∠ABD=180°.
能判断AB∥CD的是( )
 如图,点E在AC的延长线上,对于给出的四个条件:
如图,点E在AC的延长线上,对于给出的四个条件:①∠3=∠4;②∠1=∠2;③∠A=∠DCE;④∠D+∠ABD=180°.
能判断AB∥CD的是( )
| A. | ②③ | B. | ②③④ | C. | ②③ | D. | ①②③④ |
 一只跳蚤在第一象限及x轴、y轴上跳动,在第一秒钟,它从原点跳动到(0,1),然后接着按图中箭头所示方向跳动[即(0,0)→(0,1)→(1,1)→(1,0)→(2,0)…],且每秒跳动一个单位,那么第35秒时跳蚤所在位置的坐标是(5,0).
一只跳蚤在第一象限及x轴、y轴上跳动,在第一秒钟,它从原点跳动到(0,1),然后接着按图中箭头所示方向跳动[即(0,0)→(0,1)→(1,1)→(1,0)→(2,0)…],且每秒跳动一个单位,那么第35秒时跳蚤所在位置的坐标是(5,0). 下列图形中:①等腰三角形;②矩形;③正五边形;④六边形,只有三个是可以通过切正方体(如图)而得到的切口平面图形,这三个图形的序号是①②④.
下列图形中:①等腰三角形;②矩形;③正五边形;④六边形,只有三个是可以通过切正方体(如图)而得到的切口平面图形,这三个图形的序号是①②④.
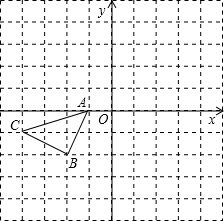 如图所示的正方形网格中,△ABC的顶点均在格点上,请在所给直角坐标系中按要求画图和解答下列问题:
如图所示的正方形网格中,△ABC的顶点均在格点上,请在所给直角坐标系中按要求画图和解答下列问题: