题目内容
如图1,点M、N分别是正方形ABCD的边AB、AD的中点,连接CN、DM.
(1)判断CN、DM的数量关系与位置关系,并说明理由;
(2)如图2,设CN、DM的交点为H,连接BH,求证:BH=BC;
(3)将△ADM沿DM翻折得到△A′DM,延长MA′交DC的延长线于点E,如图3,求cos∠DEM.
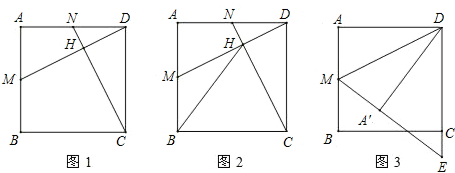
(1)判断CN、DM的数量关系与位置关系,并说明理由;
(2)如图2,设CN、DM的交点为H,连接BH,求证:BH=BC;
(3)将△ADM沿DM翻折得到△A′DM,延长MA′交DC的延长线于点E,如图3,求cos∠DEM.

考点:正方形的性质,全等三角形的判定与性质,勾股定理
专题:
分析:(1)CN=DM,CN⊥DM,由于点M、N分别是正方形ABCD的边AB、AD的中点,所以AM=DN,AD=DC,∠A=∠CDN,由此证明△AMD≌△DNC,然后利用全等三角形的性质证明 CN=DM,CN⊥DM;
(2)延长DM、CB交于点P.由AD∥BC得到∠MPC=∠MDA,而∠A=∠MBP,MA=MB,由此证明△AMD≌△BMP,然后利用全等三角形的性质即可证明题目结论;
(3)由AB∥DC,得到∠EDM=∠AMD=∠DME,接着得到EM=ED,设AD=A′D=4k,则A′M=AM=2k,那么DE=EA′+2k.而在Rt△DA′E中,A′D2+A′E2=DE2,由此可以得到关于A′E用k表示的结论,然后利用三角函数的定义即可求解.
(2)延长DM、CB交于点P.由AD∥BC得到∠MPC=∠MDA,而∠A=∠MBP,MA=MB,由此证明△AMD≌△BMP,然后利用全等三角形的性质即可证明题目结论;
(3)由AB∥DC,得到∠EDM=∠AMD=∠DME,接着得到EM=ED,设AD=A′D=4k,则A′M=AM=2k,那么DE=EA′+2k.而在Rt△DA′E中,A′D2+A′E2=DE2,由此可以得到关于A′E用k表示的结论,然后利用三角函数的定义即可求解.
解答:证明:(1)CN=DM,CN⊥DM,
∵点M、N分别是正方形ABCD的边AB、AD的中点,
∴AM=DN
在△AMD和△DNC中,
,
∴△AMD≌△DNC(SAS),
∴CN=DM.∠CND=∠AMD,
∴∠CND+∠NDM=∠AMD+∠NDM=90°,
∴CN⊥DM,
∴CN=DM,CN⊥DM;
(2)如图,
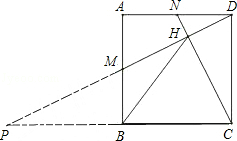
延长DM、CB交于点P.
∵AD∥BC,
∴∠MPC=∠MDA,∠A=∠MBP,
在△AMD和△BMP中
∴△AMD≌△BMP(AAS),
∴BP=AD=BC.
∵∠CHP=90°,
∴BH=BC,
(3)如图,
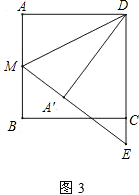
∵AB∥DC,
∴∠EDM=∠AMD=∠DME,
∴EM=ED.
设AD=A′D=4k,则A′M=AM=2k,
∴DE=ME=EA′+2k.
在Rt△DA′E中,A′D2+A′E2=DE2,
∴(4k)2+A′E2=(EA′+2k)2,
解得A′E=3k,
∴在直角△A′DE中,cos∠DEM=
.
∵点M、N分别是正方形ABCD的边AB、AD的中点,
∴AM=DN
在△AMD和△DNC中,
|
∴△AMD≌△DNC(SAS),
∴CN=DM.∠CND=∠AMD,
∴∠CND+∠NDM=∠AMD+∠NDM=90°,
∴CN⊥DM,
∴CN=DM,CN⊥DM;
(2)如图,

延长DM、CB交于点P.
∵AD∥BC,
∴∠MPC=∠MDA,∠A=∠MBP,
在△AMD和△BMP中
|
∴△AMD≌△BMP(AAS),
∴BP=AD=BC.
∵∠CHP=90°,
∴BH=BC,
(3)如图,

∵AB∥DC,
∴∠EDM=∠AMD=∠DME,
∴EM=ED.
设AD=A′D=4k,则A′M=AM=2k,
∴DE=ME=EA′+2k.
在Rt△DA′E中,A′D2+A′E2=DE2,
∴(4k)2+A′E2=(EA′+2k)2,
解得A′E=3k,
∴在直角△A′DE中,cos∠DEM=
| 3 |
| 5 |
点评:此题主要考查了正方形的性质,同时也利用了全等三角形的性质与判定、等腰三角形的性质、勾股定理及三角函数的定义,综合性比较强.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
 已知平行四边形ABCD,AB=3,AD=5.
已知平行四边形ABCD,AB=3,AD=5. 如图在圆盘的圆周上均匀的分布着0-9的10个数,箭头固定并指向0,圆盘可以任意旋转,记Pk(k=1,2…9)表示箭头落在0-k之间的概率.如P3=
如图在圆盘的圆周上均匀的分布着0-9的10个数,箭头固定并指向0,圆盘可以任意旋转,记Pk(k=1,2…9)表示箭头落在0-k之间的概率.如P3=

 如图,直线y=kx+b经过A(3,1),B(-1,-3)两点,则不等式
如图,直线y=kx+b经过A(3,1),B(-1,-3)两点,则不等式 如图,正方形ABCD,点E为BC中点,点F在CD上,∠EAF=45°,连接EF,则∠AFE的余弦值为
如图,正方形ABCD,点E为BC中点,点F在CD上,∠EAF=45°,连接EF,则∠AFE的余弦值为