题目内容
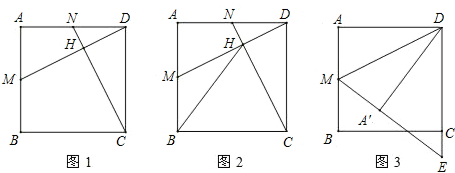
 如图,正方形ABCD,点E为BC中点,点F在CD上,∠EAF=45°,连接EF,则∠AFE的余弦值为
如图,正方形ABCD,点E为BC中点,点F在CD上,∠EAF=45°,连接EF,则∠AFE的余弦值为考点:正方形的性质,全等三角形的判定与性质,勾股定理,锐角三角函数的定义
专题:
分析:首先延长EB至H,使BH=DF,连接AH,证得△ADF≌△ABH,得出∠BAH=∠DAF,AF=AH,进一步得出△FAE≌△HAE,得出∠H=∠AFE,设BH为x,正方形的边长为a,在直角三角形ECF中利用勾股定理求得x(用a表示),进一步利用勾股定理、锐角三角函数的意义在直角三角形AHB中得出答案即可.
解答:解:如图,

延长EB至H,使BH=DF,连接AH,
∵在正方形ABCD中,
∴∠ADF=∠ABH,AD=AB,
在△ADF和△ABH中,
∴△ADF≌△ABH(SAS),
∴∠BAH=∠DAF,AF=AH,
∴∠FAH=90°,
∴∠EAF=∠EAH=45°,
在△FAE和△HAE中,
∴△FAE≌△HAE(SAS),
∴EF=HE=BE+HB=BE+DF,∠H=∠AFE,
设BH为x,正方形的边长为2a,点E为BC中点,
∴EC=a,EF=a+x,FC=2a-x
在直角三角形ECF中,
EC2+FC2=EF2
即a2+(2a-x)2=(a+x)2
解得x=
a
则AH=
=
a,
∴cos∠AFE=∠H=
=
.
故答案为:
.

延长EB至H,使BH=DF,连接AH,
∵在正方形ABCD中,
∴∠ADF=∠ABH,AD=AB,
在△ADF和△ABH中,
|
∴△ADF≌△ABH(SAS),
∴∠BAH=∠DAF,AF=AH,
∴∠FAH=90°,
∴∠EAF=∠EAH=45°,
在△FAE和△HAE中,
|
∴△FAE≌△HAE(SAS),
∴EF=HE=BE+HB=BE+DF,∠H=∠AFE,
设BH为x,正方形的边长为2a,点E为BC中点,
∴EC=a,EF=a+x,FC=2a-x
在直角三角形ECF中,
EC2+FC2=EF2
即a2+(2a-x)2=(a+x)2
解得x=
| 2 |
| 3 |
则AH=
| BH2+AB2 |
2
| ||
| 3 |
∴cos∠AFE=∠H=
| HB |
| AH |
| ||
| 10 |
故答案为:
| ||
| 10 |
点评:此题考查正方形的性质,三角形全等的判定与性质,勾股定理以及锐角三角函数的意义等知识点,注意问题的转化.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
 如图,杭州市郊外一景区内有一条笔直的公路a经过两个景点A,B,景区管委会又开发了风景优美的景点C,经测量景点C位于景点A的北偏东60°方向,又位于景点B的北偏东30°方向,且景点A、B相距200m,则景点B、C相距的路程为( )
如图,杭州市郊外一景区内有一条笔直的公路a经过两个景点A,B,景区管委会又开发了风景优美的景点C,经测量景点C位于景点A的北偏东60°方向,又位于景点B的北偏东30°方向,且景点A、B相距200m,则景点B、C相距的路程为( )A、100
| ||
| B、200 | ||
| C、100 | ||
D、200
|
在网上搜索引擎中输入“2014中考”,能搜索到与之相关的结果个数约为56400000,这个数用科学记数法表示为( )
| A、5.64×104 |
| B、5.64×105 |
| C、5.64×106 |
| D、5.64×107 |
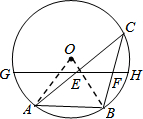 如图,AB是⊙O的一条弦,点C是⊙O上一动点,且∠ACB=30°,点E、F分别是AC、BC的中点,直线EF与⊙O交于G、H两点,若⊙O的半径为9,则GE+FH的最大值为.
如图,AB是⊙O的一条弦,点C是⊙O上一动点,且∠ACB=30°,点E、F分别是AC、BC的中点,直线EF与⊙O交于G、H两点,若⊙O的半径为9,则GE+FH的最大值为.