题目内容
1.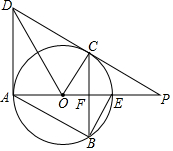 如图所示,直线DP和圆O相切于点C,交直径AE的延长线于点P.过点C作AE的垂线,交AE于点F,交圆O于点B.作平行四边形ABCD,连接BE,DO,CO.
如图所示,直线DP和圆O相切于点C,交直径AE的延长线于点P.过点C作AE的垂线,交AE于点F,交圆O于点B.作平行四边形ABCD,连接BE,DO,CO.(1)求证:DA=DC;
(2)求∠P及∠AEB的大小.
分析 (1)欲证明DA=DC,只要证明Rt△DAO≌△Rt△DCO即可;
(2)想办法证明∠P=30°即可解决问题;
解答 (1)证明:在平行四边形ABCD中,AD∥BC,
∵CB⊥AE,
∴AD⊥AE,
∴∠DAO=90°,
∵DP与⊙O相切于点C,
∴DC⊥OC,
∴∠DCO=90°,
在Rt△DAO和Rt△DCO中,
$\left\{\begin{array}{l}{DO=DO}\\{AO=CO}\end{array}\right.$,
∴Rt△DAO≌△Rt△DCO,
∴DA=DC.
(2)∵CB⊥AE,AE是直径,
∴CF=FB=$\frac{1}{2}$BC,
∵四边形ABCD是平行四边形,
∴AD=BC,
∴CF=$\frac{1}{2}$AD,
∵CF∥DA,
∴△PCF∽△PDA,
∴$\frac{PC}{PD}$=$\frac{CF}{DA}$=$\frac{1}{2}$,
∴PC=$\frac{1}{2}$PD,DC=$\frac{1}{2}$PD,
∵DA=DC,
∴DA=$\frac{1}{2}$PD,
在Rt△DAP中,∠P=30°,
∵DP∥AB,
∴∠FAB=∠P=30°,
∵AE是⊙O的直径,
∴∠ABE=90°,
∴∠AEB=60°.
点评 本题考查切线的性质、平行四边形的性质、相似三角形的判定和性质、直角三角形中30度角的判定、全等三角形的判定和性质等知识,解题的关键是正确寻找全等三角形或相似三角形解决问题,属于中考常考题型.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
11.下列计算正确的是( )
| A. | (-2a2)3=8a6 | B. | (-$\frac{1}{2}$)-1=$\frac{1}{2}$ | C. | $\sqrt{9}$=±3 | D. | a10÷a5=a5 |
12.计算(-1+2)×(-$\frac{1}{2}$)2÷(-2)的结果是( )
| A. | 8 | B. | -8 | C. | $\frac{1}{8}$ | D. | $-\frac{1}{8}$ |
10. 如图所示,该几何体的左视图是( )
如图所示,该几何体的左视图是( )
 如图所示,该几何体的左视图是( )
如图所示,该几何体的左视图是( )| A. |  | B. |  | C. |  | D. |  |
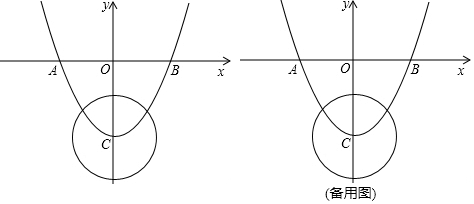
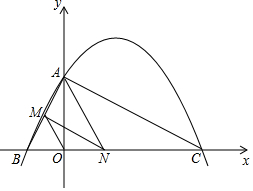 如图,已知二次函数y=ax2+bx+4的图象与x轴交于点B(-2,0),点C(8,0),与y轴交于点A.
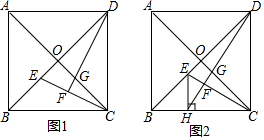
如图,已知二次函数y=ax2+bx+4的图象与x轴交于点B(-2,0),点C(8,0),与y轴交于点A.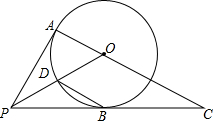 如图,PA,PB是⊙O的切线,A,B为切点,连接AO并延长,交PB的延长线于点C,连接PO,交⊙O于点D.
如图,PA,PB是⊙O的切线,A,B为切点,连接AO并延长,交PB的延长线于点C,连接PO,交⊙O于点D.