题目内容
15．
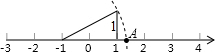如图所示：数轴上点A所表示的数为a，则a的值是（ ）| A． | $\sqrt{5}$+1 | B． | $\sqrt{5}$-1 | C． | -$\sqrt{5}$+1 | D． | -$\sqrt{5}$-1 |
分析 由勾股定理得出$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$，得出数轴上点A所表示的数是$\sqrt{5}$-1，即可得出结果．
解答 解：由勾股定理得：$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$，
∴数轴上点A所表示的数是$\sqrt{5}$-1，
∴a=$\sqrt{5}$-1；故选：B．
点评 本题考查了勾股定理、实数与数轴的关系；熟练掌握勾股定理，并能进行推理计算是解决问题的关键．
练习册系列答案
相关题目
6．已知二次函数y=x2+bx+c中，函数y与自变量x的部分对应值如下表：
（1）求该二次函数的关系式；
（2）当x为何值时，y有最小值，最小值是多少？
（3）若A（m，y1），B（m+1，y2）两点都在该函数的图象上，其中m＜1，试比较y1与y2的大小．
| x | … | -1 | 0 | 1 | 2 | 3 | 4 | … |
| y | … | 10 | 5 | 2 | 1 | 2 | 5 | … |
（2）当x为何值时，y有最小值，最小值是多少？
（3）若A（m，y1），B（m+1，y2）两点都在该函数的图象上，其中m＜1，试比较y1与y2的大小．
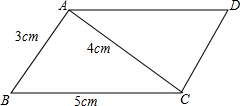求如图所示的平行四边形ABCD的面积=12cm2．
如图，∠A=40°，∠B=60°，∠D=52°，则∠E=48°．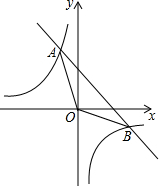
一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象交于A（-1，$\sqrt{3}$）、B（$\sqrt{3}$，n）两点．