题目内容
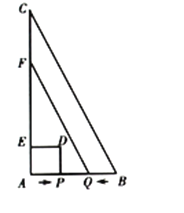
【题目】如图在△ABC中,AD是高,矩形PQMN的顶点P、N分别在AB、AC上,QM在边BC上.若BC=8cm,AD=6cm,

(1)PN=2PQ,求矩形PQMN的周长
(2)当PN为多少时矩形PQMN的面积最大,最大值为多少?
【答案】(1)矩形PQMN的周长=14.4cm;(2)当AE=3时,矩形PQMN的面积最大,最大面积是12,此时PN=4.
【解析】
(1)由题意可得出PQ:AD=BP:AB,PN:BC=AP:AB,BC=8,AD=6,据此可得出PQ,PN的值,故可得出矩形PQMN的周长;
(2)设长方形零件PQMN的边AE=x,矩形PQMN的面积为S,利用△APN∽△ABC得相似比,用相似比可得出用含x的式子表示S,从而得出二次函数解析式,根据解析式及自变量取值范围求S的最大值.
(1)由题意得;PQ:AD=BP:AB,PN:BC=AP:AB
∴![]() ,
,
又∵PN=2PQ,BC=8cm,AD=6cm,
∴![]() ,
,
∴PQ=2.4
则PN=4.8,
∴矩形PQMN的周长=14.4cm;
(2)∵四边形PQMN是矩形,
∴PN∥BC,∠PQM=90°,∠QPN=90°,
∴△PAN∽△ABC,
∵AD是高,
∴∠ADB=90°,
∴四边形PQDE是矩形,∠AEN=90°,
∴![]() ,PQ=DE,
,PQ=DE,
设AE=x,矩形PQMN的面积为S,
则![]() ,DE=6﹣x,
,DE=6﹣x,
∴PN=![]() x,PQ=6﹣x,
x,PQ=6﹣x,
∴S=﹣![]() x2+8x.
x2+8x.
∴当x=![]() =3时,S的最大值为12.,
=3时,S的最大值为12.,
∴当AE=3时,矩形PQMN的面积最大,最大面积是12,此时PN=![]() ×3=4.
×3=4.

练习册系列答案
相关题目
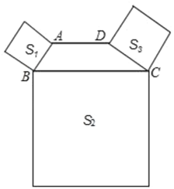
【题目】如图,四边形ABCD中,AD∥BC,∠ABC+∠DCB=90°,且BC=2AD,以AB、BC、DC为边向外作正方形,其面积分别为S1、S2、S3,若S1=2,S3=4,则S2的值为_____.