题目内容
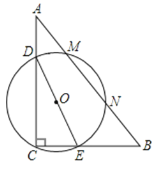
【题目】如图，在Rt△ABC中，∠C=90°，BC=6，AC=8，D、E分别是AC、BC上的一点，且DE=6 ，若以DE为直径的圆与斜边AB相交于M、N，则MN的最大值为______．
【答案】
【解析】
根据题意有C、O、G三点在一条直线上OG最小，MN最大，根据勾股定理求得AB，根据三角形面积求得CF，然后根据垂径定理和勾股定理即可求得MN的最大值．
解：过O作OG⊥AB于G，连接OC，
∵DE＝6，
∴OC＝3，只有C、O、G三点在一条直线上OG最小，
连接OM，∵OM＝3，
∴只有OG最小，GM才能最大，从而MN有最大值，
作CF⊥AB于F，
∴G和F重合时，MN有最大值，
∵∠C＝90°，BC＝6，AC＝8，
∴AB＝
＝10，
∵
ACBC＝ABCF，
∴CF＝4.8，
∴OG＝4.83＝
，
∴MG＝
=
∴MN＝2MG＝
故填：．
练习册系列答案
相关题目
